题目内容
已知一次函数y=kx+b的图象经过点P(0,-3),且与函数y=| 1 |
| 2 |
| 8 |
| 3 |
(1)求a的值;
(2)若函数y=kx+b的图象与x轴的交点是B,函数y=
| 1 |
| 2 |
分析:(1)根据一次函数y=kx+b的图象与函数y=
x+1的图象相交于点A(
,a),先求a的值,
(2)再把A、P两点的坐标代入一次函数y=kx+b中,求得k、b的值,再由题意求得B、C两点的坐标,从而求出四边形ABOC的面积.
| 1 |
| 2 |
| 8 |
| 3 |
(2)再把A、P两点的坐标代入一次函数y=kx+b中,求得k、b的值,再由题意求得B、C两点的坐标,从而求出四边形ABOC的面积.
解答:解:(1)由题意将A坐标代入y=
x+1得:a=
×
+1=
(2分)
(2)∵直线y=kx+b过点P(0,-3),A(
,
),
∴
,解得
(4分)
∴函数y=2x-3的图象与x轴的交点B(
,0),(5分)
函数y=
x+1的图象与y轴的交点C(0,1),(6分)
又S△ACP=
×4×
=
,S△BOP=
×3×
=
,(7分)
∴SABOC=S△ACP-S△BOP=
-
=
.(8分)
(注:第2小题关于四边形ABOC的面积求法较多,酌情给分)
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 3 |
| 7 |
| 3 |
(2)∵直线y=kx+b过点P(0,-3),A(
| 8 |
| 3 |
| 7 |
| 3 |
∴
|
|
∴函数y=2x-3的图象与x轴的交点B(
| 3 |
| 2 |
函数y=
| 1 |
| 2 |
又S△ACP=
| 1 |
| 2 |
| 8 |
| 3 |
| 16 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
∴SABOC=S△ACP-S△BOP=
| 16 |
| 3 |
| 9 |
| 4 |
| 37 |
| 12 |
(注:第2小题关于四边形ABOC的面积求法较多,酌情给分)
点评:本题考查了一次函数和几何问题的综合应用,主要考查平面直角坐标系中图形的面积的求法.解答此题的关键是根据一次函数的特点,分别求出各点的坐标再计算.

练习册系列答案
相关题目
 已知一次函数y=kx+2的图象经过A(-1,1).
已知一次函数y=kx+2的图象经过A(-1,1). m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.
m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.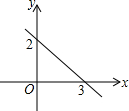 已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.
已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.