Question

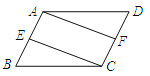
【题目】如图，在□ABCD中，E、F分别是AB、CD的中点，连接AF、CE．

（1）求证：△BEC≌△DFA；

（2）连接AC，当CA＝CB时，判断四边形AECF是什么特殊四边形？并证明你的结论．

Answer 1

【答案】（1）证明见解析；

（2）四边形AECF是矩形．

【解析】

试题分析：（1）根据平行四边形的性质推出BC=AD，∠B=∠D，AB=CD，求出BE=DF，根据SAS即可推出答案；

（2）证AE∥CF，AE=CF得到平行四边形AECF，根据等腰三角形的性质求出∠AEC=90°，根据矩形的判定即可推出答案．

试题解析：（1）∵四边形ABCD是平行四边形，

∴BC=AD，∠B=∠D，AB=CD，

∵E、F分别是AB、CD的中点，

∴BE=DF=AE=CF，

在△BEC和△DFA中，

BE=DF，∠B=∠D，BC=AD，

∴△BEC≌△DFA；

（2）四边形AECF是矩形．

∵四边形ABCD是平行四边形，

∴AB∥CD，

∵AE=CF，

∴四边形AECF是平行四边形，

∵AC=BC，E是AB的中点，

∴CE⊥AB（等腰三角形的性质），

∴∠AEC=90°，

∴平行四边形AECF是矩形．