��Ŀ����
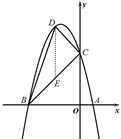
��ͼ��������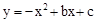 ��x�ύ��A��1��0����B��-4��0�����㣬��y����C��.
��x�ύ��A��1��0����B��-4��0�����㣬��y����C��.
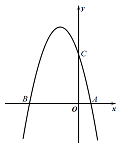
(1)��������ߵĽ���ʽ.
(2)�ڸ�������λ�ڵڶ����IJ������Ƿ���ڵ�D��ʹ�á�DBC�����S��������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�
(3)�������ߵĶ���Ϊ��F,�����߶�CF,����ֱ��BC,�����ܷ���ֱ��BC���ҵ�һ����M,�����������ҵ�һ����N,ʹ��C��F��M��N�ĵ���ɵ��ı���Ϊƽ���ı���,�����ڣ���д����M�͵�N�����ꣻ�������ڣ���˵�����ɣ�
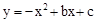 ��x�ύ��A��1��0����B��-4��0�����㣬��y����C��.
��x�ύ��A��1��0����B��-4��0�����㣬��y����C��.
(1)��������ߵĽ���ʽ.
(2)�ڸ�������λ�ڵڶ����IJ������Ƿ���ڵ�D��ʹ�á�DBC�����S��������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�
(3)�������ߵĶ���Ϊ��F,�����߶�CF,����ֱ��BC,�����ܷ���ֱ��BC���ҵ�һ����M,�����������ҵ�һ����N,ʹ��C��F��M��N�ĵ���ɵ��ı���Ϊƽ���ı���,�����ڣ���д����M�͵�N�����ꣻ�������ڣ���˵�����ɣ�
(1)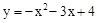 ��(2)���ڣ�(-2��,6)��(3)���ڣ�M1��
��(2)���ڣ�(-2��,6)��(3)���ڣ�M1��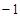 ,3����N1(
,3����N1(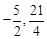 )��M2��
)��M2��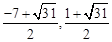 ����N2(
����N2(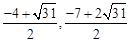 )��M3��
)��M3��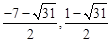 ����N3(
����N3(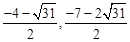 )��M4��1,5����N4(
)��M4��1,5����N4(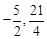 ).
).
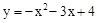 ��(2)���ڣ�(-2��,6)��(3)���ڣ�M1��
��(2)���ڣ�(-2��,6)��(3)���ڣ�M1��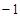 ,3����N1(
,3����N1(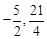 )��M2��
)��M2��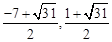 ����N2(
����N2(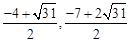 )��M3��
)��M3��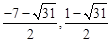 ����N3(
����N3(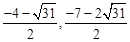 )��M4��1,5����N4(
)��M4��1,5����N4(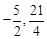 ).
).���������(1)���ݽ���ʽֱ����⣻
(2)���D������Ϊ(a,
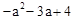 )
)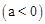 ����a��ʾ����DBC�����S���ɶ��κ�������ֵ������ɣ�
����a��ʾ����DBC�����S���ɶ��κ�������ֵ������ɣ�(3)����ƽ���ı��ε��ж���������⼴��.
���������(1)��������
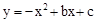 ��x�ύ��A��1��0����B��-4��0�����㣬
��x�ύ��A��1��0����B��-4��0�����㣬�������߽���ʽΪ
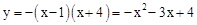 .
.(2)��ͼ�����D������Ϊ(a,
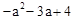 )
)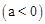 ,����D��ƽ����y���ֱ�߽�ֱ��BC�ڵ�E,
,����D��ƽ����y���ֱ�߽�ֱ��BC�ڵ�E,��C��0��4����B��-4��0���ɵ�ֱ��BC:
 �����E��a,a+4��.
�����E��a,a+4��.��S=
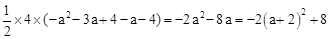 .
.�൱a=-2ʱ��S���D������Ϊ(-2��,6).
(3)���ڣ�M1��
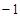 ,3����N1(
,3����N1(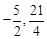 )��M2��
)��M2��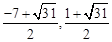 ����N2(
����N2(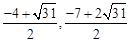 )��
)��M3��
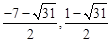 ����N3(
����N3(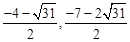 )��M4��1,5����N4(
)��M4��1,5����N4(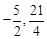 ).
).
��ϰ��ϵ�д�
 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
�����Ŀ
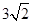 ,�������������������ߵĶ����������ߵ��ڽӸ�������ε���������,���������������ҶԳ���ƽ����y���������������
,�������������������ߵĶ����������ߵ��ڽӸ�������ε���������,���������������ҶԳ���ƽ����y���������������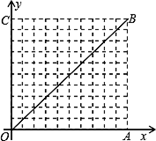
 ��
�� ��x�ύ�ڵ�A��B����y��������ύ�ڵ�C����A������Ϊ��1��0����OB=OC.
��x�ύ�ڵ�A��B����y��������ύ�ڵ�C����A������Ϊ��1��0����OB=OC.
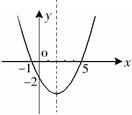
 ʱx��ֵֻ��ȡ0
ʱx��ֵֻ��ȡ0

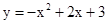 ȡ���ֵʱ��x= .
ȡ���ֵʱ��x= .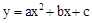 �У��亯��
�У��亯��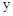 ���Ա���
���Ա���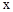 ֮��IJ��ֶ�Ӧֵ���±���ʾ��
֮��IJ��ֶ�Ӧֵ���±���ʾ��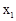 ��
��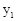 ����B��
����B�� ��
��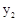 ���ں�����ͼ���ϣ���
���ں�����ͼ���ϣ���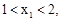
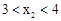 ʱ��
ʱ��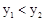 B.
B.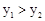 C.
C.