题目内容
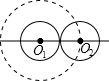如图，在同一平面上有两个大小相同的圆，其中⊙O1固定不动，⊙O2在其外围相切滚动一周，则⊙O2自转周．
- A.1
- B.2
- C.3
- D.4
B
分析：根据题意首先设⊙O1与O2半径为r，然后求得⊙O2在其外围相切滚动一周所得圆的周长与⊙O2周长，求其比值即是所求．
解答：如图：设⊙O1与O2半径为r，
∵⊙O2在其外围相切滚动一周，也滚动了一个圆，半径为2r，则它的周长为2π×2r=4πr，
又∵⊙O2周长为：2πr，
∴⊙O2自转了：4πr÷2πr=2（周）．
故选B．
点评：此题考查了圆与圆的位置关系与圆的周长的求解方法．题目难度不大，注意数形结合思想的应用．
分析：根据题意首先设⊙O1与O2半径为r，然后求得⊙O2在其外围相切滚动一周所得圆的周长与⊙O2周长，求其比值即是所求．
解答：如图：设⊙O1与O2半径为r，
∵⊙O2在其外围相切滚动一周，也滚动了一个圆，半径为2r，则它的周长为2π×2r=4πr，
又∵⊙O2周长为：2πr，
∴⊙O2自转了：4πr÷2πr=2（周）．
故选B．
点评：此题考查了圆与圆的位置关系与圆的周长的求解方法．题目难度不大，注意数形结合思想的应用．
练习册系列答案
相关题目
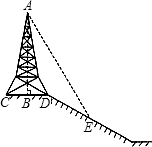如图，在斜坡的顶部有一铁塔AB，B是CD的中点，CD是水平的，在阳光的照射下，塔影DE留在坡面上．已知铁塔底座宽CD=12 m，塔影长DE=18 m，小明和小华的身高都是1.6m，同一时刻，小明站在点E处，影子在坡面上，小华站在平地上，影子也在平地上，两人的影长分别为2m和1m，那么塔高AB为（ ）
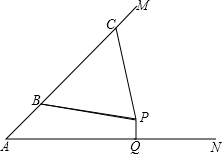如图，汶川地震后，某处废墟堆成的斜坡AM的坡度为1：1．生命探测仪显示P处有生命迹象，估计距离斜坡上的B、C处均为5米．已知水平线AN、直线AM与点P都在同一平面上，且AB=3米，BC=6米．过点P作PQ⊥AN，垂足为Q，试确定AQ和PQ的长度．
（2013•金华模拟）已知：如图，在坡度为i=1：2.4的斜坡BQ上有一棵香樟树PQ，柳明在A处测得树顶点P的仰角为α，并且测得水平的AB=8米，另外BQ=13米，tanα=0.75．点A、B、P、Q在同一平面上，PQ⊥AB．求：香樟树PQ的高度．
如图，在斜坡的顶部有一铁塔AB，B是CD的中点，CD是水平的，在阳光的照射下，塔影DE留在坡面上．已知铁塔底座宽CD=12m，塔影长DE=18m，小明和小华的身高都是1.6m，同一时刻，小明站在点E处，影子在坡面上，小华站在平地上，影子在平地上，两人的影长分别为2m和1m，求塔高AB．
下面是小民解的一道题，请你检查他的解答情况．