题目内容
 如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12m,塔影长DE=18m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子在平地上,两人的影长分别为2m和1m,求塔高AB.
如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12m,塔影长DE=18m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子在平地上,两人的影长分别为2m和1m,求塔高AB.分析:过点D构造矩形,把塔高的影长分解为平地上的BD,斜坡上的DE.然后根据影长的比分别求得AG,GB长,把它们相加即可.
解答: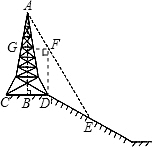 解:过D作DF⊥CD,交AE于点F,过F作FG⊥AB,垂足为G.
解:过D作DF⊥CD,交AE于点F,过F作FG⊥AB,垂足为G.
由题意得:
=
.
∴DF=DE×1.6÷2=14.4(m).
∴GF=BD=
CD=6m.
又∵
=
.
∴AG=1.6×6=9.6(m).
∴AB=14.4+9.6=24(m).
答:铁塔的高度为24m
 解:过D作DF⊥CD,交AE于点F,过F作FG⊥AB,垂足为G.
解:过D作DF⊥CD,交AE于点F,过F作FG⊥AB,垂足为G.由题意得:
| DF |
| DE |
| 1.6 |
| 2 |
∴DF=DE×1.6÷2=14.4(m).
∴GF=BD=
| 1 |
| 2 |
又∵
| AG |
| GF |
| 1.6 |
| 1 |
∴AG=1.6×6=9.6(m).
∴AB=14.4+9.6=24(m).
答:铁塔的高度为24m
点评:本题考查了运用所学的解直角三角形的知识解决实际生活中的问题,要求我们要具备数学建模能力(即将实际问题转化为数学问题).

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
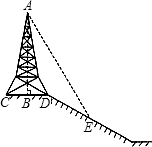 如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为( )
如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为( ) 17、如图,在斜坡的顶部有一铁塔AB,在阳光的照射下,塔影DE留在坡面上,已知铁塔底座宽CD=14m,塔影长DE=36m,小明和小华的身高都是1.6m,小明站在点E处,影子也在斜坡面上,小华站在沿DE方向的坡脚下,影子在平地上,两人的影长分别为4m与2m,那么求塔高AB.
17、如图,在斜坡的顶部有一铁塔AB,在阳光的照射下,塔影DE留在坡面上,已知铁塔底座宽CD=14m,塔影长DE=36m,小明和小华的身高都是1.6m,小明站在点E处,影子也在斜坡面上,小华站在沿DE方向的坡脚下,影子在平地上,两人的影长分别为4m与2m,那么求塔高AB. 如图,在斜坡的顶部有一铁塔AB,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=14m,塔影长DE=36m,小明和小华的身高都是1.6m,小明站在点E处,影子也在斜坡面上,小华站在沿DE方向的坡脚下,影子在平地上,两人的影长分别为4m与2m,那么,塔高AB=
如图,在斜坡的顶部有一铁塔AB,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=14m,塔影长DE=36m,小明和小华的身高都是1.6m,小明站在点E处,影子也在斜坡面上,小华站在沿DE方向的坡脚下,影子在平地上,两人的影长分别为4m与2m,那么,塔高AB= ,
, 是
是 的中点,
的中点, 留在坡面上.已知铁塔底座宽
留在坡面上.已知铁塔底座宽 ,塔影长
,塔影长 ,小明和小华的身高都是1.5m, 同一时刻,小明站在点
,小明和小华的身高都是1.5m, 同一时刻,小明站在点 处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为
处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为 和
和 ,那么塔高
,那么塔高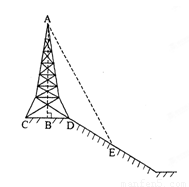
 .22m
.22m  .13.5m
.13.5m  .24m
.24m