题目内容
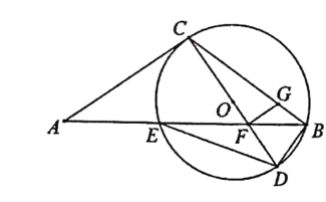
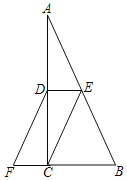
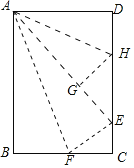
【题目】在数学拓展课《折叠矩形纸片》上,小林发现折叠矩形纸片ABCD可以进行如下操作:①把△ABF翻折,点B落在C边上的点E处,折痕为AF,点F在BC边上;②把△ADH翻折,点D落在AE边上的点G处,折痕为AH,点H在CD边上,若AD=6,CD=10,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
利用翻折不变性可得AE=AB=10,推出DE=8,EC=2,设BF=EF=x,在Rt△EFC中,x2=22+(6-x)2,可得x=![]() ,设DH=GH=y,在Rt△EGH中,y2+42=(8-y)2,可得y=3,由此即可解决问题.
,设DH=GH=y,在Rt△EGH中,y2+42=(8-y)2,可得y=3,由此即可解决问题.
∵四边形ABCD是矩形,
∴∠C=∠D=90°,AB=CD=10,AD=BC=6,
由翻折不变性可知:AB=AE=10,AD=AG=6,BF=EF,DH=HG,
∴EG=4,
在Rt△ADER中,DE=![]() =8,
=8,
∴EC=10﹣8=2,
设BF=EF=x,在Rt△EFC中有:x2=22+(6﹣x)2,
∴x=![]() ,
,
设DH=GH=y,在Rt△EGH中,y2+42=(8﹣y)2,
∴y=3,
∴EH=5,
∴ ,
,
故选A.

 阅读快车系列答案
阅读快车系列答案【题目】为监控某条生产线上产品的质量,检测员每隔相同时间抽取一件产品,并测量其尺寸(![]() ),在一天的抽检结束后,检测员将测得的各数据按从小到大的顺序整理成如下表格:
),在一天的抽检结束后,检测员将测得的各数据按从小到大的顺序整理成如下表格:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
尺寸 | 8.72 | 8.88 | 8.92 | 8.93 | 8.94 | 8.96 | 8.97 | 8.98 |
| 9.03 | 9.04 | 9.06 | 9.07 | 9.08 |
|
按照生产标准,产品等级规定如下:
尺寸(单位: | 产品等次 |
| 特等品 |
| 优等品 |
| 合格品 |
| 非合格品 |
注:在统计优等品个数时,将特等品计算在内;在统计合格个数时,将优等品(含特等品)算在内,
(1)已知此次抽检的合格率为![]() ,请判断编号为15的产品是否为合格品,并说明理由;
,请判断编号为15的产品是否为合格品,并说明理由;
(2)已知此次及抽检出的优等品尺寸的中位数为![]() .
.
①![]() __________;
__________;
②将这些优等品分成两组,一组尺寸大于![]() ,另一种尺寸不大于
,另一种尺寸不大于![]() ,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.
,从这两组中各随机抽取1件进行复检,求抽到的2件产品都是特等品的概率.