��Ŀ����
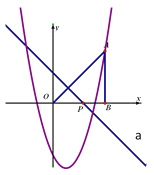
����Ŀ����ֱ��������ABC������AB=16cm��AC=12cm��BC=20cm����P�ӵ�A��ʼ��2����/����ٶ���A��B��C�ķ����ƶ�����Q�ӵ�C��ʼ��1����/����ٶ���C��A��B�ķ����ƶ��������P��Qͬʱ��������t���룩��ʾ�ƶ�ʱ������ô��
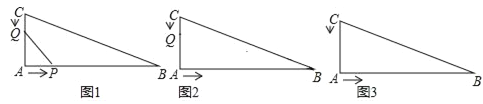
��1����ͼ1�����ú�t�Ĵ���ʽ��ʾ��������Q��AC��ʱ��CQ= ��������Q��AB��ʱ��AQ= ��
������P��AB��ʱ��BP= ��������P��BC��ʱ��BP= ��
��2����ͼ2������P���߶�AB���˶�����Q���߶�CA���˶�����QA=APʱ�������t��ֵ��
��3����ͼ3����P�㵽��C��ʱ��P��Q���㶼ֹͣ�˶�����AQ=BPʱ�������t��ֵ��
���𰸡���1��t��t��12��16��2t��2t��16����2��t=4����3��t=4��t=![]() ��
��
�������������������1�����������εı߳�������˶��ٶȽ��
��2�����������г����̣��ⷽ�̼��ɣ�
��3���ֵ�P���߶�AB���˶�����Q���߶�CA���˶�����P���߶�BC���˶�����Q���߶�CA���˶�����P���߶�BC���˶�����Q���߶�AB���˶���������г����̣��ⷽ�̼��ɣ�
�����������1���ٵ���Q��AC��ʱ��CQ=t��
�ڵ���Q��AB��ʱ��AQ=t-12��
�۵���P��AB��ʱ��BP=16-2t��
�ܵ���P��BC��ʱ��BP=2t-16��
�ʴ�Ϊ��t��t-12��16-2t��2t-16��
��2��������ã�12-t=2t��
��ã�t=4��
��3����AQ=BP
�൱��P���߶�AB���˶�����Q���߶�CA���˶�ʱ��12-t=16-2t��
��ã�t=4��
����P���߶�BC���˶�����Q���߶�CA���˶�ʱ��12-t=2t-16��
��ã�t=![]() ��
��
����P���߶�BC���˶�����Q���߶�AB���˶�ʱ��t-12=2t-16��
��ã�t=4���������⣩
��t=4��t=![]() ʱ��AQ=BP��
ʱ��AQ=BP��