题目内容
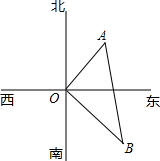 如图,在水塔O的东北方向10m处有一抽水站A,在水塔的东南方向20
如图,在水塔O的东北方向10m处有一抽水站A,在水塔的东南方向20| 2 |
分析:先求出点A、B的坐标,过点A作x轴的垂线,过点B作y中的垂线,相交于点C,然后求出AC、BC的长,再利用勾股定理列式计算即可得解.
解答: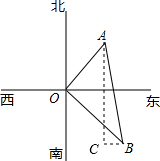 解:∵A在水塔O的东北方向10m,B在水塔O的东南方向20
解:∵A在水塔O的东北方向10m,B在水塔O的东南方向20
m,
∴A(5
,5
),B(20,-20),
如图,过点A作x轴的垂线,过点B作y中的垂线,
则AC=(20+5
)m,BC=(20-5
)m,
根据勾股定理,AB=
=
=
=30m,
即水管的长为30m.
 解:∵A在水塔O的东北方向10m,B在水塔O的东南方向20
解:∵A在水塔O的东北方向10m,B在水塔O的东南方向20| 2 |
∴A(5
| 2 |
| 2 |
如图,过点A作x轴的垂线,过点B作y中的垂线,
则AC=(20+5
| 2 |
| 2 |
根据勾股定理,AB=
| AC2+BC2 |
(20+5
|
| 900 |
即水管的长为30m.
点评:本题考查了二次根式的应用,方向角,求出点A、B的坐标并作辅助线构造出以AB为斜边的直角三角形是解题的关键.

练习册系列答案
相关题目
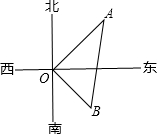 如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为( )
如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为( )| A、45m | B、40m | C、50m | D、56m |
 如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
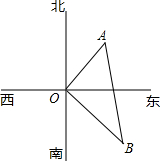 如图,在水塔O的东北方向10m处有一抽水站A,在水塔的东南方向20
如图,在水塔O的东北方向10m处有一抽水站A,在水塔的东南方向20 m处有一建筑工地B,在AB间铺设一条直通的水管,求水管的长.
m处有一建筑工地B,在AB间铺设一条直通的水管,求水管的长.