题目内容
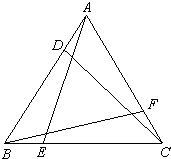 3、如图,在等边三角形ABC中,D、E、F是边AB、BC、AC上的点,且都不是中点,若AD=BE=CF,连接AE、BF、CD构成一些三角形.如果三个全等的三角形组成“全等三角形组”,那么图中“全等三角形组”的组数是( )
3、如图,在等边三角形ABC中,D、E、F是边AB、BC、AC上的点,且都不是中点,若AD=BE=CF,连接AE、BF、CD构成一些三角形.如果三个全等的三角形组成“全等三角形组”,那么图中“全等三角形组”的组数是( )分析:根据等边三角形的性质推出∠BAC=∠ABC=∠ACB=60°,AB=BC=AC,根据全等三角形的性质和判定证出即可.
解答:解:∵等边三角形ABC,
∴∠BAC=∠ABC=∠ACB=60°,AB=BC=AC,
∵AD=BE=CF,
∴△ABE≌△BCF≌△CAD,
∴∠BAE=∠CBF=∠ACD,∠ADC=∠AEB=∠BFC,
∵AD=BE=CF,
∴△ADQ≌△BEM≌△CFN,
∴AQ=BM=CN,
∵∠ABC=∠BAC=∠ACB,∠BAE=∠CBF=∠ACD,
∴∠QAC=∠NCB=∠MBA,
∵AB=BC=AC,BM=CN=AQ,
∴△AMB≌△CQA≌△BNC,
∵AB=AC=BC,AD=BE=CF,
∴BD=CE=AF,
∵∠BAC=∠ACB=∠ABC,AB=CB=AC,
∴△ABF≌△CAE≌△BCD,
∵AM=BN=CQ,∠FAM=∠ECQ=∠DBN,BD=AF=CE,
∴△AMF≌△CQE≌△BND,
∴共5组,
故选B.
∴∠BAC=∠ABC=∠ACB=60°,AB=BC=AC,
∵AD=BE=CF,
∴△ABE≌△BCF≌△CAD,
∴∠BAE=∠CBF=∠ACD,∠ADC=∠AEB=∠BFC,
∵AD=BE=CF,

∴△ADQ≌△BEM≌△CFN,
∴AQ=BM=CN,
∵∠ABC=∠BAC=∠ACB,∠BAE=∠CBF=∠ACD,
∴∠QAC=∠NCB=∠MBA,
∵AB=BC=AC,BM=CN=AQ,
∴△AMB≌△CQA≌△BNC,
∵AB=AC=BC,AD=BE=CF,
∴BD=CE=AF,
∵∠BAC=∠ACB=∠ABC,AB=CB=AC,
∴△ABF≌△CAE≌△BCD,
∵AM=BN=CQ,∠FAM=∠ECQ=∠DBN,BD=AF=CE,
∴△AMF≌△CQE≌△BND,
∴共5组,
故选B.
点评:本题主要考查对全等三角形的性质和判定,等边三角形的性质等知识点的理解和掌握,能熟练地根据全等三角形的性质和判定进行推理是解此题的关键.

练习册系列答案
相关题目
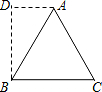 如图,在等边三角形ABC中,BD⊥BC,过A作AD⊥BD于D,已知△ABC周长为M,则AD=( )
如图,在等边三角形ABC中,BD⊥BC,过A作AD⊥BD于D,已知△ABC周长为M,则AD=( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在等边三角形ABC的边BC、AC上分别取点D、E,使BD=CE,AD与BE相交于点P.则∠APE的度数为
如图,在等边三角形ABC的边BC、AC上分别取点D、E,使BD=CE,AD与BE相交于点P.则∠APE的度数为 9、如图,在等边三角形ABC中,三条中线AE,BD,CF相交于点O,则等边三角形ABC中,从△BOF到△COD需要经过的变换是( )
9、如图,在等边三角形ABC中,三条中线AE,BD,CF相交于点O,则等边三角形ABC中,从△BOF到△COD需要经过的变换是( ) 如图,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD,求证:△BDE为等腰三角形.
如图,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD,求证:△BDE为等腰三角形. 如图,在等边三角形△ABC中,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,且PR=PS,下面给出的四个结论:①点P在∠A的平分线上,②AS=AR,③QP∥AR,④△BRP≌△QSP,则其中正确的是( )
如图,在等边三角形△ABC中,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,且PR=PS,下面给出的四个结论:①点P在∠A的平分线上,②AS=AR,③QP∥AR,④△BRP≌△QSP,则其中正确的是( )