��Ŀ����
��������ͼ����ͼ�д������ε�����ɱ�ʾΪ��a+b��2��Ҳ�ɱ�ʾΪc2+4��(| 1 |
| 2 |
| 1 |
| 2 |
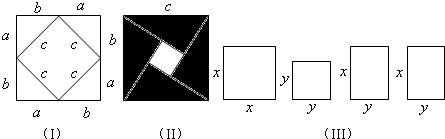
��1��������ͼ����2002��������ּҴ���꣩���������ʽ��֤���ɶ����������ĸ�ֱ�������εĽϴ��ֱ�DZ߳���Ϊa����С��ֱ�DZ߳���Ϊb��б�߳���Ϊc����
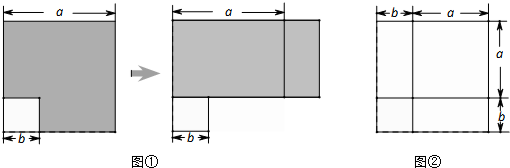
��2�������ã����ṩ��ͼ�ν�����ϣ������ͼ�ε��������ʽ��֤����x+y��2=x2+2xy+y2��
��������1����Ӱ��������ɴ������������ȥС�����������Ҳ�������ĸ�ֱ�����������֮�������������ȼ��ɵ�֤��
��2��ƴ����ͼ��ʾͼ�Σ����������α߳�Ϊx+y����ʾ���������������������С�������������������֮�������������֤��
��2��ƴ����ͼ��ʾͼ�Σ����������α߳�Ϊx+y����ʾ���������������������С�������������������֮�������������֤��
��� �⣺��1��S��Ӱ=4��
�⣺��1��S��Ӱ=4��
ab��S��Ӱ=c2-��a-b��2��
��4��
ab=c2-��a-b��2����2ab=c2-a2+2ab-b2��
��a2+b2=c2��
��2����ͼ��ʾ��
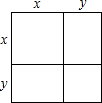
�������ε����Ϊx2+y2+2xy��Ҳ����Ϊ��x+y��2��
��x+y��2=x2+2xy+y2��
 �⣺��1��S��Ӱ=4��
�⣺��1��S��Ӱ=4��| 1 |
| 2 |
��4��
| 1 |
| 2 |
��a2+b2=c2��
��2����ͼ��ʾ��
�������ε����Ϊx2+y2+2xy��Ҳ����Ϊ��x+y��2��
��x+y��2=x2+2xy+y2��
���������⿼������ʽ�Ļ�����㣬�����������㷨���ǽⱾ��Ĺؼ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ