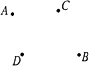Question

如图所示，在开阔地带有四个村庄A、B、C、D饮水困难，现准备建一水厂，向这四个村庄同时送水，问该水厂建在何处时，所需水管最短？请说明理由．

Answer 1

答案：
解析：

解：连接点A、B及C、D，水厂建在线段AB、CD的交点O处． 　　理由如下，如图， 　　令AB、CD交于点O．另取异于O的一点M，连接MA、MB、MC、MD．根据三角形三边关系，有MA＋MB＞AB．MC＋MD＞CD，所以MA＋MB＋MC＋MD＞AB＋CD．故水厂建在AB、CD交点O处时，所需水管最短． 　　本题也可以根据“两点之间，线段最短”作出解答．