题目内容
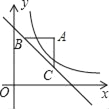
【题目】如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是_____.
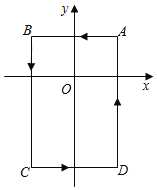
【答案】(1,0)
【解析】
根据点的坐标求出四边形ABCD的周长,然后求出另一端是绕第几圈后的第几个单位长度,从而确定答案.
∵A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),
∴AB=1﹣(﹣1)=2,BC=1﹣(﹣2)=3,CD=1﹣(﹣1)=2,DA=1﹣(﹣2)=3,
∴绕四边形ABCD一周的细线长度为2+3+2+3=10,
2019÷10=201…9,
∴细线另一端在绕四边形第202圈的第9个单位长度的位置,
即细线另一端所在位置的点的坐标是(1,0).
故答案为:(1,0).

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目