题目内容
【题目】如图24,在平面直角坐标系中,圆D与![]() 轴相切于点C(0,4),与
轴相切于点C(0,4),与![]() 轴相交于A、B两点,且AB=6
轴相交于A、B两点,且AB=6
(1)D点的坐标是 ,圆的半径为 ;
(2)求经过C、A、B三点的抛物线所对应的函数关系式;
(3)设抛物线的顶点为F,试证明直线AF与圆D相切;
(4)在![]() 轴下方的抛物线上,是否存在一点N,使
轴下方的抛物线上,是否存在一点N,使![]() 面积最大,最大面积是多少?并求出
面积最大,最大面积是多少?并求出![]() 点坐标.
点坐标.

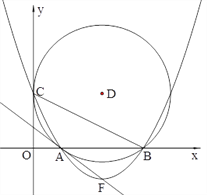
【答案】(1)(5,4), 5;
(2)![]() ;
;
(3)证明见解析;
(4)存在点N,使![]() 面积最小,当a=4时,
面积最小,当a=4时, ![]() 最大,最大值为16,此时,N(4,-2)
最大,最大值为16,此时,N(4,-2)
【解析】(1)连接DC,则DC⊥y轴,过点D作DE⊥AB于点E,则根据垂径定理可得AE=BE=3,连接DA,在Rt△ADE中可求出DA,即圆的半径,也可得出点D的坐标;
(2)利用待定系数法可求出经过C、A、B三点的抛物线的解析式.
(3)因为D为圆心,A在圆周上,DA=r=5,故只需证明∠DAF=90°,利用勾股定理的逆定理证明∠DAF=90°即可.
(4)设存在点N,过点N作NP与y轴平行,交BC于点P,求出直线BC的解析式,设点N坐标(a, ![]() ),则可得点P的坐标为(a,
),则可得点P的坐标为(a, ![]() a+4),从而根据S△BCN=S△BPN+S△PCN,表示出△BCN的面积,利用配方法可确定最大值,继而可得出点N的坐标.
a+4),从而根据S△BCN=S△BPN+S△PCN,表示出△BCN的面积,利用配方法可确定最大值,继而可得出点N的坐标.
解:(1)解:连接DC,则DC⊥y轴,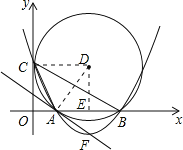
过点D作DE⊥AB于点E,则DE垂直平分AB,
∵AB=6,∴AE=3,
在Rt△ADE中,AD=![]() =5,
=5,
故可得点D的坐标为(5,4),圆的半径为5;
(2)解:设经过点A、B、C三点的抛物线解析式为:y=ax2+bx+c,
将三点坐标代入可得: 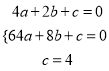 ,解得:
,解得: ![]() ,
,
故经过C、A、B三点的抛物线的解析式为:y=![]() .
.
(3)证明:因为D为圆心,A在圆周上,DA=r=5,故只需证明∠DAF=90°,
抛物线顶点坐标:F(5, ![]() ),DF=4+
),DF=4+![]() =
=![]() ,AF=
,AF=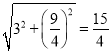 ,
,
∵DA2+AF2=52+(![]() )2=
)2=![]() =(
=(![]() )2=DF2,
)2=DF2,
∴∠DAF=90°
所以AF切于圆D.
(4)解:存在点N,使△CBN面积最大.
根据点B及点C的坐标可得:直线BC的解析式为:y=![]() x+4,
x+4,
设N点坐标(a, ![]() ),过点N作NP与y轴平行,交BC于点P,
),过点N作NP与y轴平行,交BC于点P,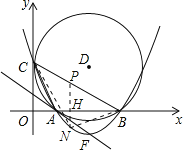
可得P点坐标为(a, ![]() x+4),
x+4),
则NP=![]() a+4-(
a+4-(![]() )=
)=![]() ,
,
故S△BCN=S△BPN+S△PCN=![]() ×PN×OH+
×PN×OH+![]() ×PN×BH=
×PN×BH=![]() PN×BO=
PN×BO=![]() ×8×(
×8×(![]() a2+2a)=16-(a-4)2
a2+2a)=16-(a-4)2
当a=4时,S△BCN最大,最大值为16,此时,N(4,-2).
“点睛”本题考查了二次函数及圆的综合,涉及了垂径定理、抛物线求二次函数解析式、切线的判定与性质,综合考察的知识点较多,同学们注意培养自己解答综合题的能力,关键还是基础知识的掌握,要能将所学知识融会贯通,第四问解法不止一种,同学们可以积极探索其他解法.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案