Question

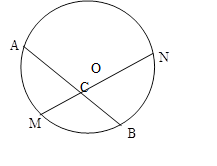
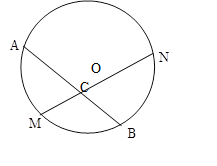
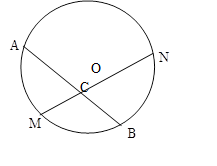
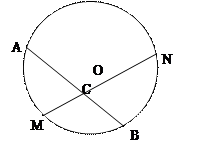
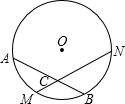已知：如图，M是弧AB的中点，过点M的弦MN交弦AB于点C，设⊙O的半径为4cm，MN=4

3

cm．
（1）求圆心O到弦MN的距离；
（2）猜想OM和AB的位置关系，并说明理由；
（3）求∠ACM的度数．

Answer 1

分析：（1）连接OM，由垂径定理可知MD=ND，在Rt△MOD中，已知OM、MD，易求OD．
（2）连接OA、OB，由于M是弧AB的中点，易证∠AOM=∠BOM，又OA=OB，利用等腰三角形三线合一的性质，易证OM⊥AB．
（3）利用锐角三角函数，易求∠OMD=30°，进而易求∠ACM=60°．

解答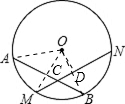：解：（1）连接OM，
∵点M是弧AB的中点，
∴OM⊥AB，过点O作OD⊥MN于点D，
由垂径定理，得MD=

1

2

MN=2

3

．
在Rt△ODM中，OM=4，MD=2

3

，
∴OD=

OM2-MD2

=2
故圆心O到弦MN的距离为2cm．

（2）猜想：OM⊥AB
连接OA、OB，由M是弧AB的中点，
得∠AOM=∠BOM，
又因为OA=OB，所以OM⊥AB．

（3）cos∠OMD=

MD

OM

=

3

2

，
∴∠OMD=30°，
∵OM⊥AB，
∴∠ACM=60°．

点评：本题主要考查了垂径定理，此类在圆中涉及弦长、半径、圆心角的计算的问题，常把半弦长，半圆心角，圆心到弦距离转换到同一直角三角形中，然后通过直角三角形予以求解，常见辅助线是过圆心作弦的垂线．