题目内容
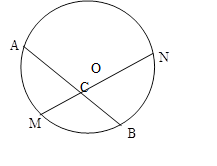
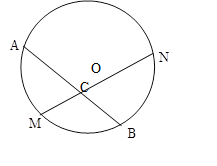
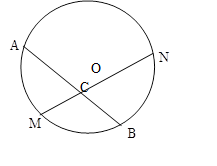
已知，如图，M是弧AB的中点，过点M的弦MN交于点C，设圆O的半径为4厘米，MN=4cm,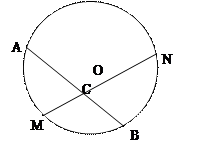
(1)求圆心O到弦MN的距离；
(2)求∠ACM的度数。
略解析:
解：(1)连接OM. ∵点M是AB的中点，∴OM⊥AB.过点O作OD⊥MN于点D，
由垂径定理，得MD=1/2MN=
∴在Rt△ODM中,OM=4,MD=
∴OD=2.故圆心O到弦MN的距离为2…………….5分
(2)cos∠OMD="MD:OM" =
,∴∠OMD=30°,∴∠ACM= 60°………..3分
解：(1)连接OM. ∵点M是AB的中点，∴OM⊥AB.过点O作OD⊥MN于点D，
由垂径定理，得MD=1/2MN=
∴在Rt△ODM中,OM=4,MD=∴OD=2.故圆心O到弦MN的距离为2…………….5分
(2)cos∠OMD="MD:OM" =
,∴∠OMD=30°,∴∠ACM= 60°………..3分 
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
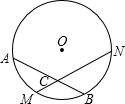已知：如图，M是弧AB的中点，过点M的弦MN交弦AB于点C，设⊙O的半径为4cm，MN=4
