题目内容
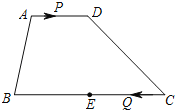
【题目】如图,在梯形ABCD中,AD∥BC,AD=4,BC=12,E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.当运动时间为 秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
【答案】2或![]() .
.
【解析】
试题分析:分别从当Q运动到E和B之间与当Q运动到E和C之间去分析,根据平行四边形的性质,可得方程,继而可求得答案.
解:∵E是BC的中点,
∴BE=CE=![]() BC=
BC=![]() ×12=6,
×12=6,
①当Q运动到E和C之间,设运动时间为t,则AP=t,DP=AD﹣AP=4﹣t,CQ=2t,EQ=CE﹣CQ=6﹣2t,
∴4﹣t=6﹣2t,
解得:t=2;
②当Q运动到E和B之间,设运动时间为t,则AP=t,DP=AD﹣AP=4﹣t,CQ=2t,EQ=CQ﹣CE=2t﹣6,
∴4﹣t=2t﹣6,
解得:t=![]() ,
,
∴当运动时间t为2或![]() 秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
故答案为:2或![]() .
.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目