题目内容
已知两直线y1=kx+k-1、y2=(k+1)x+k(k为正整数),设这两条直线与x轴所围成的三角形的面积为Sk,则S1+S2+S3+…+S2013的值是
- A.

- B.
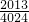
- C.
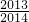
- D.
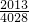
D
分析:方程组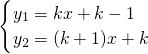 的解为
的解为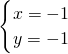 ,直线y1=kx+k-1与x轴的交点为(
,直线y1=kx+k-1与x轴的交点为(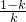 ,0),y2=(k+1)x+k与x轴的交点为(
,0),y2=(k+1)x+k与x轴的交点为( 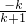 ,0),先计算出SK的面积,再依据规律求解.
,0),先计算出SK的面积,再依据规律求解.
解答:∵方程组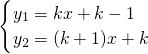 的解为
的解为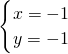 ,
,
∴两直线的交点是(-1,-1),
∵直线y1=kx+k-1与x轴的交点为(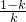 ,0),y2=(k+1)x+k与x轴的交点为(
,0),y2=(k+1)x+k与x轴的交点为(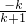 ,0),
,0),
∴Sk= ×|-1|×|
×|-1|×|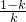 -
-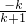 |=
|= |
| -
- |,
|,
∴S1+S2+S3+…+S2013=(1- +
+ -
- +
+ -
- +…+
+…+ -
-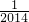 )
)
= ×(1-
×(1-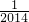 )
)
= ×
×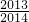
=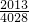 .
.
故选D.
点评:本题考查的是一次函数图象上点的坐标特点.熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.
分析:方程组
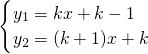 的解为
的解为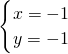 ,直线y1=kx+k-1与x轴的交点为(
,直线y1=kx+k-1与x轴的交点为(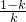 ,0),y2=(k+1)x+k与x轴的交点为(
,0),y2=(k+1)x+k与x轴的交点为( 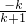 ,0),先计算出SK的面积,再依据规律求解.
,0),先计算出SK的面积,再依据规律求解.解答:∵方程组
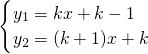 的解为
的解为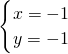 ,
,∴两直线的交点是(-1,-1),
∵直线y1=kx+k-1与x轴的交点为(
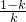 ,0),y2=(k+1)x+k与x轴的交点为(
,0),y2=(k+1)x+k与x轴的交点为(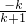 ,0),
,0),∴Sk=
 ×|-1|×|
×|-1|×|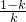 -
-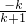 |=
|= |
| -
- |,
|,∴S1+S2+S3+…+S2013=(1-
 +
+ -
- +
+ -
- +…+
+…+ -
-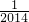 )
)=
 ×(1-
×(1-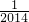 )
)=
 ×
×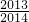
=
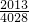 .
.故选D.
点评:本题考查的是一次函数图象上点的坐标特点.熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知反比例函数
已知反比例函数