题目内容
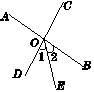
如图,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.

(1)请你数一数,图中有_________个小于平角的角;
(2)若∠AOC=50°,则∠COE的度数=_________,∠BOE的度数=_________;
(3)猜想:OE是否平分∠BOC?请通过计算说明你猜想的结论.

(1)请你数一数,图中有_________个小于平角的角;
(2)若∠AOC=50°,则∠COE的度数=_________,∠BOE的度数=_________;
(3)猜想:OE是否平分∠BOC?请通过计算说明你猜想的结论.
(1)9;(2)65°,65°;(3)OE平分∠BOC
试题分析:(1)根据角的表示方法结合图形的特征即可得到结果;
(2)由∠AOC=50°结合角平分线的性质可求得∠AOD、∠DOC的度数,再结合∠DOE=90°即可求得结果;
(3)设∠AOC=2α,根据角平分线的性质可得∠AOD=∠COD=
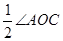 =α,再根据∠DOE=90°可表示出∠COE、∠BOE的度数,从而作出判断.
=α,再根据∠DOE=90°可表示出∠COE、∠BOE的度数,从而作出判断.(1)图中有∠AOD、∠DOC、∠COE、∠BOE、∠AOC、∠DOE、∠COB、∠AOE、∠DOB共9个小于平角的角;
(2)∵∠AOC=50°,OD平分∠AOC
∴∠AOD=∠DOC=
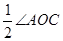 =25°
=25°∵∠DOE=90°
∴∠COE=∠DOE-∠COD=65°,∠BOE=180°-∠DOE-∠AOD=65°;
(3)结论:OE平分∠BOC.
理由:设∠AOC=2α,
∵OD平分∠AOC,∠AOC=2α,
∴∠AOD="∠COD" =
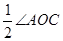 =α,
=α, 又∵∠DOE=90°
∴∠COE=∠DOE-∠COD=90°-α.
又∵∠BOE=180°-∠DOE-∠AOD=180°-90°-α=90°-α,
∴∠COE=∠BOE,即OE平分∠BOC.
点评:解题的关键是熟练掌握角的平分线把角分成相等的两个小角,且都等于大角的一半.

练习册系列答案
相关题目


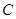 为线段
为线段 的中点,
的中点,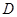 在线段
在线段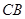 上,
上,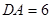 ,
,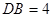 ,则
,则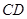 的长度是______.
的长度是______.
