题目内容
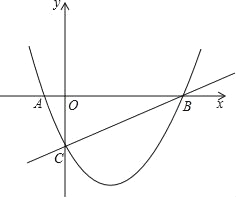
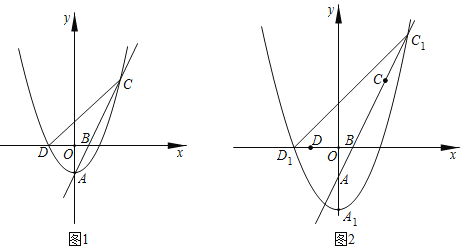
【题目】如图1，抛物线W：y＝ax2﹣2的顶点为点A，与x轴的负半轴交于点D，直线AB交抛物线W于另一点C，点B的坐标为（1，0）．
（1）求直线AB的解析式；
（2）过点C作CE⊥x轴，交x轴于点E，若AC平分∠DCE，求抛物线W的解析式；
（3）若a＝
，将抛物线W向下平移m（m＞0）个单位得到抛物线W1，如图2，记抛物线W1的顶点为A1，与x轴负半轴的交点为D1，与射线BC的交点为C1．问：在平移的过程中，tan∠D1C1B是否恒为定值？若是，请求出tan∠D1C1B的值；若不是，请说明理由．
【答案】（1）y＝2x﹣2；（2）y＝
x2﹣2；（3）tan∠D1C1B恒为定值，
，见解析
【解析】
（1）由待定系数法可求解析式；
（2）如图1，过点
作
于
，通过证明
，可得
，由平行线分线段成比例可求
，可得
，
，设
，
，则
，
，由勾股定理可求
，可求点
，点
坐标，代入解析式可求
的值，即可求抛物线
的解析式；
（3）先求出点
的坐标
，如图2，过点作
轴，过点作
轴，可证
，可得
，如图3，过点作
于点
，由勾股定理和直角三角形的性质可求
，
，
的长，即可求
．
解：（1）∵抛物线W：y＝ax2﹣2的顶点为点A，
∴点A（0，﹣2）
设直线AB解析式为y＝kx+b，
∴
解得
∴抛物线解析式为：y＝2x﹣2；
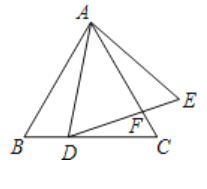
（2）如图1，过点B作BN⊥CD于N，
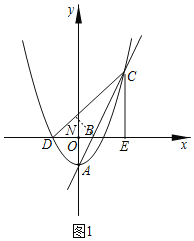
∵AC平分∠DCE，BN⊥CD，BE⊥CE，
∴BN＝BE，
∵∠BND＝∠CED＝90°，∠BDN＝∠CDE，
∴△BND∽△CED，
∴，
∴
，
∵AO∥CE，
∴
＝
∴CE＝2BE，CD＝2DB，
设BE＝x，BD＝y，则CE＝2x，CD＝2y，
∵CD2＝DE2+CE2，
∴4y2＝（x+y）2+4x2，
∴（x+y）（5x﹣3y）＝0，
∴y＝
x，
∴点C（x+1，2x），点D（1﹣x，0）
∵点C，点D是抛物线W：y＝ax2﹣2上的点，
∴
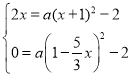
∴x+1＝（1﹣x）2，
∴x1＝0（舍去），x2＝
，
∴0＝a（1﹣
）2﹣2，
∴a＝，
∴抛物线解析式为：y＝x2﹣2；
（3）tan∠D1C1B恒为定值，
理由如下：由题意可得抛物线W1的解析式为：y＝
x2﹣2﹣m，
设点D1的坐标为（t，0）（t＜0），
∴0＝t2﹣2﹣m，
∴2+m＝t2，
∴抛物线W1的解析式为：y＝x2﹣t2，
∵抛物线W1与射线BC的交点为C1，
∴
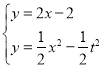
解得：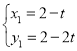
，
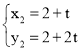（不合题意舍去），
∴点C1的坐标（2﹣t，2﹣2t），
如图2，过点C1作C1H⊥x轴，过点C作CG⊥x轴，
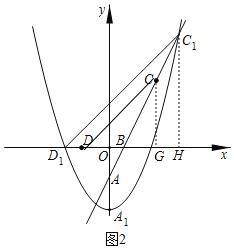
∴C1H＝2﹣2t，OH＝2﹣t，
∴D1H＝D1O+OH＝2﹣t+（﹣t）＝2﹣2t，
∴C1H＝D1H，且C1H⊥x轴，
∴∠C1D1H＝45°，
∵y＝x2﹣2与x轴交于点D，
∴点D（﹣2，0）
∵y＝2x﹣2与y＝x2﹣2交于点C，点A
∴点C（4，6）
∴GC＝6，DG＝OD+OG＝2+4＝6，
∴DG＝CG，且CG⊥x轴，
∴∠GDC＝45°＝∠C1D1H，
∴C1D1∥CD，
∴∠D1C1B＝∠DCB，
∴tan∠D1C1B＝tan∠DCB，
如图3，过点B作BF⊥CD于点F，
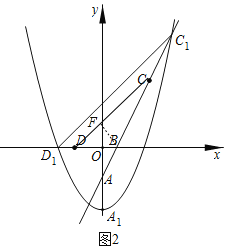
∵∠CDB＝45°，BF⊥CD，BD＝OD+OB＝2+1＝3，
∴∠FDB＝∠FBD＝45°，
∴DF＝BF，DB＝
DF＝3，
∴DF＝BF＝
∵点D（﹣2，0），点C（4，6），
∴CD＝
＝6，
∴CF＝CD﹣DF＝
，
∴tan∠D1C1B＝tan∠DCB＝
＝，
∴tan∠D1C1B恒为定值．
