题目内容
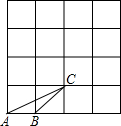 如图,每个小方格的边长都是1,请你在图中画一个格点三角形A′B′C′(三顶点在格点上),使
如图,每个小方格的边长都是1,请你在图中画一个格点三角形A′B′C′(三顶点在格点上),使△A′B′C′∽△ABC,且△A′B′C′的面积为
| 5 | 2 |
分析:首先根据△A′B′C′∽△ABC,△A′B′C′的面积为
,得出两三角形的面积之比为:
:
=1:5,进而得出两三角形的相似之比为:1:
,求出各边长,画出图形即可.
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
解答: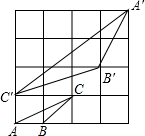 解:如图所示:∵每个小方格的边长都是1,
解:如图所示:∵每个小方格的边长都是1,
∴△ABC的面积为
×1×1=
,
∵△A′B′C′∽△ABC,△A′B′C′的面积为
,
∴两三角形的面积之比为:
:
=1:5,
∴两三角形的相似之比为:1:
,
∴
=
=
=
,
∴可求得:A′B′=
,B′C′=
,A′C′=5,
进而画出图形即可.
 解:如图所示:∵每个小方格的边长都是1,
解:如图所示:∵每个小方格的边长都是1,∴△ABC的面积为
| 1 |
| 2 |
| 1 |
| 2 |
∵△A′B′C′∽△ABC,△A′B′C′的面积为
| 5 |
| 2 |
∴两三角形的面积之比为:
| 1 |
| 2 |
| 5 |
| 2 |
∴两三角形的相似之比为:1:
| 5 |
∴
| AB |
| A′B′ |
| BC |
| B′C′ |
| AC |
| A′C′ |
| 1 | ||
|
∴可求得:A′B′=
| 5 |
| 10 |
进而画出图形即可.
点评:此题主要考查了作相似图形,根据相似三角形的性质得出三角形各边长是解题关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
 8、如图,每个小方格的边长为1,如果E点的坐标是(-2,3),那么原点最可能在( )的位置.
8、如图,每个小方格的边长为1,如果E点的坐标是(-2,3),那么原点最可能在( )的位置.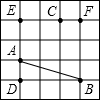 已知如图,每个小方格的边长为1,以A、B、C、D、E、F其中的三个点,能否找到三边长都是无理数三角形?如能,请你在图中连好线;点C到线段AB的距离等于多少?
已知如图,每个小方格的边长为1,以A、B、C、D、E、F其中的三个点,能否找到三边长都是无理数三角形?如能,请你在图中连好线;点C到线段AB的距离等于多少?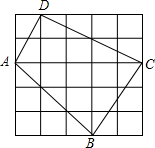 如图,每个小方格的边长都为1.求图中格点四边形ABCD的面积.
如图,每个小方格的边长都为1.求图中格点四边形ABCD的面积. 如图,每个小方格的边长为单位1,将△ABC沿AD平移,且使A点平移到D点,B、C平移后的对应点分别为E、F.
如图,每个小方格的边长为单位1,将△ABC沿AD平移,且使A点平移到D点,B、C平移后的对应点分别为E、F.