题目内容
如图,已知AB是⊙O直径,AC是⊙O弦,点D是 的中点,弦DE⊥AB,垂足为F,DE交AC于点G.
的中点,弦DE⊥AB,垂足为F,DE交AC于点G.(1)若过点E作⊙O的切线ME,交AC的延长线于点M(请补完整图形),试问:ME=MG是否成立?若成立,请证明;若不成立,请说明理由;
(2)在满足第(2)问的条件下,已知AF=3,FB=
 ,求AG与GM的比.
,求AG与GM的比.
【答案】分析:(1)连接OE,并延长EO交⊙O于N,连接DN;由于ME是⊙O的切线,则∠MEG=∠N,而∠MGE=∠AGF,易证得∠AGF=∠B,即∠MGE=∠B,若证ME=MG,关键就是证得∠N=∠B;可从题干入手:点D是弧ABC的中点,则弧AD=弧DBC=弧AE,所以弧DBE=弧AEC,即AC=DE,由此可证得∠N=∠B,即可得到∠MGE=∠MEG,根据等角对等边即可得证.
(2)根据相交弦定理可求得DF、EF的长,即可得到DE、AC的长,易证得△AFG∽△ACB,根据所得比例线段即可求得AG、GC的长,再由(1)证得ME=MG,可用MG分别表示出MA、MC的长,进而根据切割线定理求出MG的长,有了AG、MG的值,那么它们的比例关系就不难求出.
解答: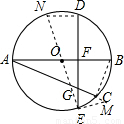 解:(1)ME=MG成立,理由如下:
解:(1)ME=MG成立,理由如下:
如图,连接EO,并延长交⊙O于N,连接BC;
∵AB是⊙O的直径,且AB⊥DE,
∴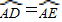 ,
,
∵点D是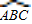 的中点,
的中点,
∴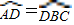 ,
,
∴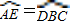 ,
,
∴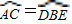 ,即AC=DE,∠N=∠B;
,即AC=DE,∠N=∠B;
∵ME是⊙O的切线,
∴∠MEG=∠N=∠B,
又∵∠B=90°-∠GAF=∠AGF=∠MGE,
∴∠MEG=∠MGE,故ME=MG.
(2)由相交弦定理得:DF2=AF•FB=3× =4,即DF=2;
=4,即DF=2;
故DE=AC=2DF=4;
∵∠FAG=∠CAB,∠AFG=∠ACB=90°,
∴△AFG∽△ACB,
∴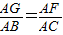 ,即
,即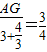 ,
,
解得AG=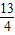 ,GC=AC-AG=
,GC=AC-AG= ;
;
设ME=MG=x,则MC=x- ,MA=x+
,MA=x+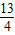 ,
,
由切割线定理得:ME2=MC•MA,即x2=(x- )(x+
)(x+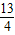 ),
),
解得MG=x=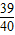 ;
;
∴AG:MG=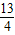 :
: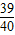 =10:3,即AG与GM的比为
=10:3,即AG与GM的比为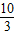 .
.
点评:此题是一道圆的综合题,涉及到:切线的性质、圆周角定理、相交弦定理、弦切角定理、切割线定理等重要知识点,综合性强,难度较大,能够发现AC、DE的等量关系是解答此题的关键所在.
(2)根据相交弦定理可求得DF、EF的长,即可得到DE、AC的长,易证得△AFG∽△ACB,根据所得比例线段即可求得AG、GC的长,再由(1)证得ME=MG,可用MG分别表示出MA、MC的长,进而根据切割线定理求出MG的长,有了AG、MG的值,那么它们的比例关系就不难求出.
解答:
 解:(1)ME=MG成立,理由如下:
解:(1)ME=MG成立,理由如下:如图,连接EO,并延长交⊙O于N,连接BC;
∵AB是⊙O的直径,且AB⊥DE,
∴
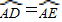 ,
,∵点D是
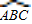 的中点,
的中点,∴
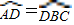 ,
,∴
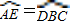 ,
,∴
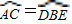 ,即AC=DE,∠N=∠B;
,即AC=DE,∠N=∠B;∵ME是⊙O的切线,
∴∠MEG=∠N=∠B,
又∵∠B=90°-∠GAF=∠AGF=∠MGE,
∴∠MEG=∠MGE,故ME=MG.
(2)由相交弦定理得:DF2=AF•FB=3×
 =4,即DF=2;
=4,即DF=2;故DE=AC=2DF=4;
∵∠FAG=∠CAB,∠AFG=∠ACB=90°,
∴△AFG∽△ACB,
∴
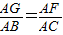 ,即
,即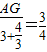 ,
,解得AG=
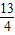 ,GC=AC-AG=
,GC=AC-AG= ;
;设ME=MG=x,则MC=x-
 ,MA=x+
,MA=x+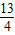 ,
,由切割线定理得:ME2=MC•MA,即x2=(x-
 )(x+
)(x+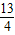 ),
),解得MG=x=
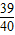 ;
;∴AG:MG=
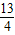 :
: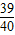 =10:3,即AG与GM的比为
=10:3,即AG与GM的比为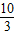 .
.点评:此题是一道圆的综合题,涉及到:切线的性质、圆周角定理、相交弦定理、弦切角定理、切割线定理等重要知识点,综合性强,难度较大,能够发现AC、DE的等量关系是解答此题的关键所在.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°,BD=10.
如图,已知AB是⊙O的直径,AC是弦,D为AB延长线上一点,DC=AC,∠ACD=120°,BD=10. 如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F. (2013•泰安)如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是
(2013•泰安)如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是
 如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC.
如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC. 如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.
如图,已知AB是圆O的直径,∠DAB的平分线AC交圆O与点C,作CD⊥AD,垂足为点D,直线CD与AB的延长线交于点E.