题目内容
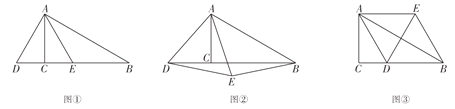
【题目】探究:如图1和图2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.
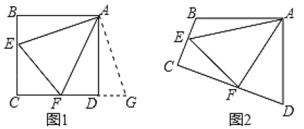
(1)①如图1,若∠B、∠ADC都是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,直接写出线段BE、DF和EF之间的数量关系;
②如图2,若∠B、∠D都不是直角,则当∠B与∠D满足 关系时,线段BE、DF和EF之间依然有①中的结论存在,请你写出该结论的证明过程;
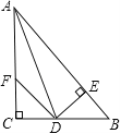
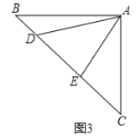
(2)拓展:如图3,在△ABC中,∠BAC=90°,AB=AC=2![]() ,点D、E均在边BC上,且∠DAE=45°,若BD=1,求DE的长.
,点D、E均在边BC上,且∠DAE=45°,若BD=1,求DE的长.
【答案】(1)①EF=BE+DF;②∠B+∠D=180°,理由见解析;(2)DE=![]()
【解析】
(1)①根据旋转的性质得出AE=AG,∠BAE=∠DAG,BE=DG,求出∠EAF=∠GAF=45°,根据SAS推出△EAF≌△GAF,根据全等三角形的性质得出EF=GF,即可求出答案;
②根据旋转的性质作辅助线,得出AE=AG,∠B=∠ADG,∠BAE=∠DAG,求出C、D、G在一条直线上,根据SAS推出△EAF≌△GAF,根据全等三角形的性质得出EF=GF,即可求出答案;
(2)如图3,同理作旋转三角形,根据等腰直角三角形性质和勾股定理求出∠ABC=∠C=45°,BC=4,根据旋转的性质得出AF=AE,∠FBA=∠C=45°,∠BAF=∠CAE,求出∠FAD=∠DAE=45°,证△FAD≌△EAD,根据全等得出DF=DE,设DE=x,则DF=x,BF=CE=3﹣x,根据勾股定理得出方程,求出x即可.
(1)①如图,
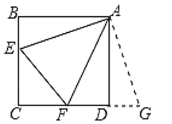
∵把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,
∴AE=AG,∠BAE=∠DAG,BE=DG,∠B=∠ADG=90°,
∵∠ADC=90°,
∴∠ADC+∠ADG=90°
∴F、D、G共线,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠DAG+∠DAF=45°,
即∠EAF=∠GAF=45°,
在△EAF和△GAF中,
∵ ,
,
∴△EAF≌△GAF(SAS),
∴EF=GF,
∵BE=DG,
∴EF=GF=DF+DG=BE+DF;
②∠B+∠D=180°,
理由是:
如图2,把△ABE绕A点旋转到△ADG,使AB和AD重合,
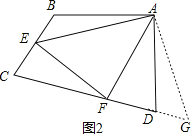
则AE=AG,∠B=∠ADG,∠BAE=∠DAG,
∵∠B+∠ADC=180°,
∴∠ADC+∠ADG=180°,
∴C、D、G在一条直线上,
与①同理得,∠EAF=∠GAF=45°,
在△EAF和△GAF中
 ,
,
∴△EAF≌△GAF(SAS),
∴EF=GF,
∵BE=DG,
∴EF=GF=BE+DF;
故答案为:∠B+∠D=180°;
(2)∵△ABC中,AB=AC=2![]() ,∠BAC=90°,
,∠BAC=90°,
∴∠ABC=∠C=45°,
由勾股定理得:BC=![]() ,
,
如图3,把△AEC绕A点旋转到△AFB,使AB和AC重合,连接DF.
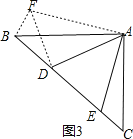
则AF=AE,∠FBA=∠C=45°,∠BAF=∠CAE,
∵∠DAE=45°,
∴∠FAD=∠FAB+∠BAD=∠CAE+∠BAD=∠BAC﹣∠DAE=90°﹣45°=45°,
∴∠FAD=∠DAE=45°,
在△FAD和△EAD中
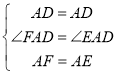 ,
,
∴△FAD≌△EAD(SAS),
∴DF=DE,
设DE=x,则DF=x,
∵BC=4,
∴BF=CE=4﹣1﹣x=3﹣x,
∵∠FBA=45°,∠ABC=45°,
∴∠FBD=90°,
由勾股定理得:DF2=BF2+BD2,
即x2=(3﹣x)2+12,
解得:x=![]() ,
,
即DE=![]() .
.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案