题目内容
【题目】如图,已知平行四边形ABCD,DE是∠ADC的角平分线,交BC于点E.
(1)求证:CD=CE;
(2)若BE=CE,∠B=80°,求∠DAE的度数.
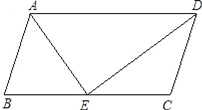
【答案】(1)证明见解析;(2)∠DAE=50°.
【解析】试题分析:(1)根据DE是∠ADC的角平分线得到∠1=∠2,再根据平行四边形的性质得到∠1=∠3,所以∠2=∠3,根据等角对等边即可得证;
(2)先根据BE=CE结合CD=CE得到△ABE是等腰三角形,求出∠BAE的度数,再根据平行四边形邻角互补得到∠BAD=100°,所以∠DAE可求.
(1)证明:如图,在平行四边形ABCD中,
∵AD∥BC
∴∠1=∠3
又∵∠1=∠2,
∴∠2=∠3,
∴CD=CE;
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
又∵CD=CE,BE=CE,
∴AB=BE,
∴∠BAE=∠BEA.
∵∠B=80°,
∴∠BAE=50°,
∴∠DAE=180°﹣50°﹣80°=50°.
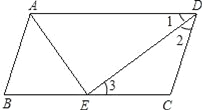
点睛:本题主要考查平行四边形的性质,根据平行四边形的性质中对边平行,以及DE是∠ADC的平分线,证明△DEC是等腰三角形,以类似的方法也可以求出∠DAE的角度.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目