Question

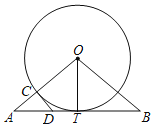
【题目】如图所示，△ABC内接于⊙O，且AB为⊙O的直径，作的平分线交圆周于点D，连结AD、BD，AB、CD交于点E．

（1）求证：△ABD为等腰直角三角形；

（2）填空：

①若，则AE的长度为_______；

②在①的条件下，延长AC、DB交于点P，则______．

Answer 1

【答案】（1）见解析；（2）①；②6．

【解析】

（1）由AB为直径，则，由角平分线和圆周角定理，得到，即可得到结论；

（2）①作，则，由三角形的面积之比，得到，然后求出AB的长度，即可得到答案；

②由题意，先证明△ADP∽△BCP，则，根据比例进行计算，即可得到答案．

（1）证明:∵CD平分

∴

∵

∴

∴

∵AB为⊙O的直径

∴

∴△ABD为等腰直角三角形;

（2）作，如图1所示：

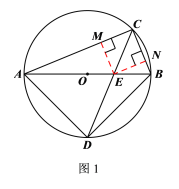
∵CD平分，，

∴

∵，

∴，

∴，

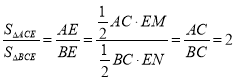在Rt△ABC（AB为⊙O的直径）中，由勾股定理得:

∴；

故答案为：；

②如图：

由①可知，，△ABD为等腰直角三角形，

∴，

∵∠ADB=∠BCP=90°，∠P=∠P，

∴△ADP∽△BCP，

∴，

∵，，

∴，

解得：，，

故答案为：6；