题目内容
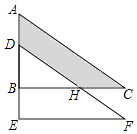
【题目】如图(1),在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF,连接CF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图(2),线段CF,BD所在直线的位置关系为______,线段CF,BD的数量关系为________;
②当点D在线段BC的延长线上时,如图(3),①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.

【答案】(1)①CF⊥BD;CF=BD,②成立,理由见解析;(2)∠ACB=45°时,CF⊥BC
【解析】试题分析:(1)当点D在BC的延长线上时①的结论仍成立.由正方形ADEF的性质可推出△DAB≌△FAC,所以CF=BD,∠ACF=∠ABD.结合∠BAC=90°,AB=AC,得到∠BCF=∠ACB+∠ACF=90度.即CF⊥BD.
(2)当∠ACB=45°时,过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,可推出∠ACB=∠AGC,所以AC=AG,由(1)①可知CF⊥BD.
试题解析:
(1)①结合∠BAC=90°,AB=AC,得到∠BCF=∠ACB+∠ACF=90度.即CF⊥BD.当点D在BC的延长线上时①的结论仍成立.由正方形ADEF的性质可推出△DAB≌△FAC,所以CF=BD.
②当点D在BC的延长线上时①的结论仍成立.
由正方形ADEF得AD=AF,∠DAF=90度.
∵∠BAC=90°,
∴∠DAF=∠BAC,
∴∠DAB=∠FAC,
又∵AB=AC,
∴△DAB≌△FAC,
∴CF=BD,∠ACF=∠ABD.
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ACF=45°,
∴∠BCF=∠ACB+∠ACF=90度.
即CF⊥BD.
(2)当∠ACB=45°时,CF⊥BD(如图).
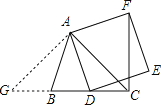
理由:过点A作AG⊥AC交CB的延长线于点G,
则∠GAC=90°,
∵∠ACB=45°,∠AGC=90°-∠ACB,
∴∠AGC=90°-45°=45°,
∴∠ACB=∠AGC=45°,
∴AC=AG,
∵∠DAG=∠FAC(同角的余角相等),AD=AF,
∴△GAD≌△CAF,
∴∠ACF=∠AGC=45°,
∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案【题目】在信息快速发展的社会,“信息消费”已成为人们生活的重要组成部分.某高校组织课外小组在郑州市的一个社区随机抽取部分家庭,调查每月用于信息消费的金额,根据数据整理成如图所示的不完整统计表和统计图.已知A,B两组户数频数直方图的高度比为1:5.
月信息消费额分组统计表
组别 | 消费额(元) |
A | 10≤x<100 |
B | 100≤x<200 |
C | 20≤x<300 |
D | 300≤x<400 |
E | x≥400 |
请结合图表中相关数据解答下列问题:
(1)这次接受调查的有 户;
(2)在扇形统计图中,“E”所对应的圆心角的度数是 ;
(3)请你补全频数直方图;
(4)若该社区有2000户住户,请估计月信息消费额不少于200元的户数是多少?