题目内容
【题目】如图,∠BAC=90°,AB=AC,D点在AC上,E点在BA的延长线上,BD=CE,BD的延长线交CE于F.证明: 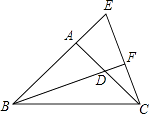
(1)AD=AE
(2)BF⊥CE.
【答案】
(1)证明:∵∠BAC=90°,
∴∠CAE=∠BAC=90°,
在Rt△BAD和Rt△CAE中
![]()
∴Rt△BAD≌Rt△CAE(HL),
∴AD=AE
(2)证明:由(1)可知Rt△BAD≌Rt△CAE,
∴∠ADB=∠E,
∵∠ABD+∠ADB=90°,
∴∠ABD+∠E=90°,
∴∠BFE=90°,即BF⊥CE.
【解析】(1)可证明Rt△BAD≌Rt△CAE,可证得AD=AE;(2)利用(1)中的全等,可知∠E=∠ADB,结合条件可求得∠ABD+∠E=90°,可证明BF⊥CE.

练习册系列答案
相关题目