题目内容
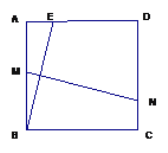
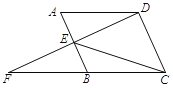
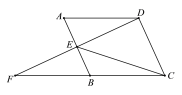
【题目】如图，□ABCD中，点E是AB边的中点，延长DE交CB的延长线于点F．
⑴ 求证：△ADE≌△BFE；
⑵ 若DE⊥AB且DE＝AB，连接EC，求∠FEC的度数．
【答案】⑴ 见解析；⑵ ∠FEC=135°
【解析】
（1）由平行四边形的性质证得∠A=∠FBE，∠ADE=∠F，再由点E是AB中点，得AE=BE，即证得△ADE≌△BFE；
（2）由□ABCD得AB∥DC，AB=CD ，由DE⊥AB且DE＝AB易证∠CDF=90°，可得∠DEC =45°，从而可得结论.
⑴ ∵ 四边形ABCD是平行四边形
∴ AD∥BC
∴ ∠A=∠ABF
∵ 点E是AB的中点
∴ AE=BE
在△ABE和△ACD中
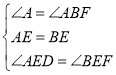
∴ △ADE≌△BFE
⑵ ∵ 四边形ABCD是平行四边形
∴ AB∥DC，AB=CD
∴ ∠CDF=∠BEF
∵ DE⊥AB
∴ ∠BEF=90°
∴ ∠CDF=90°
∵ DE=AB
∴ DE=DC
∴ ∠DEC=∠DCE=45°
∴ ∠FEC=135°
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
