题目内容
 20、如图,已知在?ABCD中,对角线AC,BD相交于点O,点E、F是AC上两点,点E、F的位置只须满足条件
20、如图,已知在?ABCD中,对角线AC,BD相交于点O,点E、F是AC上两点,点E、F的位置只须满足条件
AE=CF
时,四边形DEBF是平行四边形.分析:根据?ABCD,得出DO=BO,AO=CO,再根据对角线互相平分的四边形是平行四边形,得出四边形DEBF是平行四边形.
解答: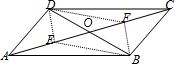 解:在?ABCD中,对角线AC,BD相交于点O,点E、F是AC上两点,点E、F的位置只须满足,CF=AE,四边形DEBF是平行四边形.
解:在?ABCD中,对角线AC,BD相交于点O,点E、F是AC上两点,点E、F的位置只须满足,CF=AE,四边形DEBF是平行四边形.
∵在?ABCD中,
∴DO=BO,AO=CO,
又∵AE=CF,
∴EO=FO,
∴四边形DEBF是平行四边形.
故答案为:AE=CF.
 解:在?ABCD中,对角线AC,BD相交于点O,点E、F是AC上两点,点E、F的位置只须满足,CF=AE,四边形DEBF是平行四边形.
解:在?ABCD中,对角线AC,BD相交于点O,点E、F是AC上两点,点E、F的位置只须满足,CF=AE,四边形DEBF是平行四边形.∵在?ABCD中,
∴DO=BO,AO=CO,
又∵AE=CF,
∴EO=FO,
∴四边形DEBF是平行四边形.
故答案为:AE=CF.
点评:此题主要考查了平行四边形的性质与判定方法,正确应用对角线互相平分判定平行四边形是解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
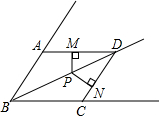 如图,已知在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.
如图,已知在△ABC中,BD为∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD于M,PN⊥CD于N,求证:PM=PN.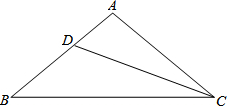 如图,已知在△ABC中,AB=AC,∠A=100°,CD是∠ACB的平分线.
如图,已知在△ABC中,AB=AC,∠A=100°,CD是∠ACB的平分线.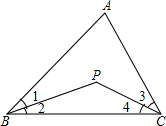 如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠A=70°时,则∠BPC的度数为
如图,已知在△ABC中,∠B与∠C的平分线交于点P.当∠A=70°时,则∠BPC的度数为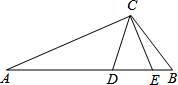 如图,已知在△ABC中,CD=CE,∠A=∠ECB,试说明CD2=AD•BE.
如图,已知在△ABC中,CD=CE,∠A=∠ECB,试说明CD2=AD•BE.