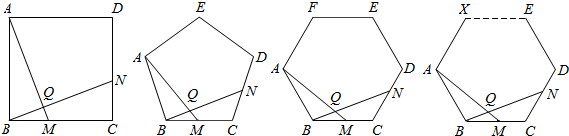
题目内容
已知正五边形ABCDE的周长为2000米，甲、乙两人分别从A、C同时出发，沿A→B→C→D→E→A→…方向绕广场行走，甲的速度为50米/分，乙的速度为46米/分，那么出发后经过多少分钟，甲、乙两人第一次开始行走在同一条边上．
解：∵正五边形ABCDE的周长为2000米，
∴边长为400米，
设x分钟后，甲、乙两人2人均在五边形的顶点，第一次开始行走在同一条边上．
50x-46x=400，
解得x=100．
此时甲走了5000米，
5000÷400=12…200米，
还有200米才到五边形的一个顶点，
200÷50=4分，
∵4分钟后乙还在这一边上，
∴104分后，甲、乙两人第一次开始行走在同一条边上．
答：104分后，甲、乙两人第一次开始行走在同一条边上．
分析：先求得每边的长，若2人均在五边形的顶点可得等量关系为：甲所走的路程-乙走的路程=1边长，把相关数值代入计算即可．
点评：考查推理与论证的应用；得到甲乙两人路程的等量关系是解决本题的关键．
∴边长为400米，
设x分钟后，甲、乙两人2人均在五边形的顶点，第一次开始行走在同一条边上．
50x-46x=400，
解得x=100．
此时甲走了5000米，
5000÷400=12…200米，
还有200米才到五边形的一个顶点，
200÷50=4分，
∵4分钟后乙还在这一边上，
∴104分后，甲、乙两人第一次开始行走在同一条边上．
答：104分后，甲、乙两人第一次开始行走在同一条边上．
分析：先求得每边的长，若2人均在五边形的顶点可得等量关系为：甲所走的路程-乙走的路程=1边长，把相关数值代入计算即可．
点评：考查推理与论证的应用；得到甲乙两人路程的等量关系是解决本题的关键．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
相关题目
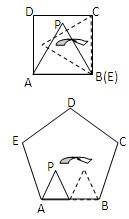16、如图，已知正方形ABCD的边长AB=1，正△PAE的边长AE=1，开始时正△PAE与正方形ABCD边AB重合，顶点P在正方形内，将正△PAE在正方形内按如图所示的方式，沿着正方形的边AB、BC、CD、DA、AB、BC…连续地翻转
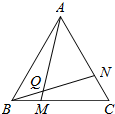（1）已知△ABC为正三角形，点M是BC上一点，点N是AC上一点，AM、BN相交于点Q，∠BAM=∠NBC，猜想∠BQM等于多少度，并证明你的猜想．
