题目内容
(1)已知:如图1,△ABC为正三角形,点M、N分别在BC、CA边上,且BM=CN,BN与AM相交于Q点,试求∠BQM的度数.解:∵△ABC为正三角形,∴∠ABC=∠ACB=60°,AB=BC.
在△ABM和△BCN中,
|
∴∠
∴∠BQM=∠
(2)如果将(1)中的正三角形改为正方形ABCD(如图2),点M、N分别在BC、CD边上,且BM=CN,BN与AM相交于Q点,那么∠BQM等于多少度呢?说明理由.

(3)如果将(1)中的“正三角形”改为正五边形、正六边形、…、正n边形(如图3),其余条件都不变,请你根据(1)(2)的求解思路,将你推断的结论填入下表:(正多边形的各个内角都相等)
| 正多边形 | 正五边形 | 正六边形 | … | 正n边形 |
| ∠BQM的度数 | … |
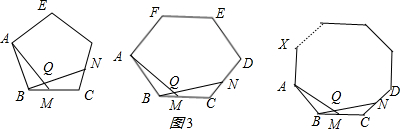
分析:(1)根据等边三角形的性质,三条边都相等,三个角都是直角找出条件,然后利用“边角边”定理证明△ABM和△BCN全等,再根据全等三角形对应角相等得到∠BAM=∠CBN,然后即可证明∠BQM=∠ABQ+∠CBN=60°;
(2)同(1)的思路先证明△ABM和△BCN全等,再根据全等三角形对应角相等得到∠BAM=∠CBN,然后即可证明∠BQM=∠ABQ+∠CBN=90°;
(3)根据规律,∠BQM的度数等于正多边形的一个内角的度数,然后分别求出各多边形的内角的度数即可.
(2)同(1)的思路先证明△ABM和△BCN全等,再根据全等三角形对应角相等得到∠BAM=∠CBN,然后即可证明∠BQM=∠ABQ+∠CBN=90°;
(3)根据规律,∠BQM的度数等于正多边形的一个内角的度数,然后分别求出各多边形的内角的度数即可.
解答:解:(1)故答案为:
,(SAS),∠BAM=∠CBN,
∠BAQ+∠ABQ,∠ABQ+∠QBM,60;
(2)∵ABCD为正方形,
∴∠ABC=∠BCD=90°,AB=BC,
在△ABM和△BCN中,
?△ABM≌△BCN(SAS),
∴∠BAQ=∠QBM,
∴∠BQM=∠BAQ+∠ABQ=∠ABQ+∠QBM=90°;
(3)108°,120°,180°-
或
.
|
∠BAQ+∠ABQ,∠ABQ+∠QBM,60;
(2)∵ABCD为正方形,
∴∠ABC=∠BCD=90°,AB=BC,
在△ABM和△BCN中,
|
∴∠BAQ=∠QBM,
∴∠BQM=∠BAQ+∠ABQ=∠ABQ+∠QBM=90°;
(3)108°,120°,180°-
| 360° |
| n |
| (n-2)•180° |
| n |
点评:本题考查了全等三角形的判定与性质,等边三角形的性质,正方形的性质,以及多边形的内角的求法,规律性较强,难度不大,希望同学们熟练掌握.

练习册系列答案
相关题目
 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上. 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为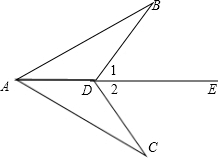 已知,如图,∠1=∠2,
已知,如图,∠1=∠2, 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为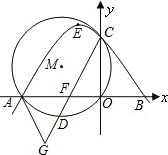 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧