Question

在平面直角坐标系内，O为坐标原点，点C坐标为（0，

3

），E点坐标为（1，0），将△COE沿直线CE折叠，点O落在点D处．
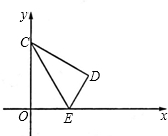（1）求直线CE的解析式；
（2）求点D的坐标；
（3）以CE为底边，且底角为30°的等腰三角形有几个？请写出这些等腰三角形顶点的坐标．

Answer 1

（1）设直线CE的解析式为y=kx+b（k≠0）．
∵点C坐标为（0，

3

），E点坐标为（1，0），
∴

3 =b 0=k+b

，
解得k=-

3

，b=

3

，即直线CE的解析式为y=-

3

x+

3

；

（2）Rt△COE中，OE=1、OC=

3

，
∴∠OCE=30°，则∠OCD=60°；
又CO=CD，
∴△OCD是等边三角形，作高DF⊥y轴垂足F，则OF=

1

2

OC=

3

2

，DF=

3

OF=

3

2

，
则点D坐标（

3

2

，

3

2

）；

（3）以CE为底边且底角30°的等腰三角形有两个：①△JCE，点J（1，

2 3

3

）；②△KCE，点K（0，

3

3

）．