题目内容
【题目】为调查某校学生一学期课外书的阅读量情况，从全校学生中随机抽取50名学生的阅读情况进行分析，并规定如下：设一个学生一学期阅读课外书籍本数为n，当0≤n＜5时，该学生为一般读者；当5≤n＜10时，该学生为良好读者；当n≥10时，该学生为优秀读者．
随机抽取的50名学生一学期阅读课外书的本数数据如下：
阅读本数n | 0 | 2 | 4 | 5 | 6 | 8 | 10 | 12 | 14 | 16 |
人数 | 1 | 1 | 2 | 3 | 12 | 11 | 5 | 8 | 5 | 2 |
根据以上数据回答下列问题：
（1）请你估计在全校学生中任意抽取一个学生，是良好读者的概率是多少？（直接写出结果）
（2）在样本中为一般读者的学生中随机抽取2人，用树状图或列表法求抽得2人的课外书籍阅读本数都为4本的概率．
【答案】（1）
；（2）
．
【解析】
试题分析：（1）由给出的数据可求出当5≤n＜10时的人数，进而可求得良好读者的概率；
（2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与抽得2人的课外书籍阅读本数都为4的情况，再利用概率公式即可求得答案．
解：
（1）∵5≤n＜10时，学生的人数为3+12+11=26（人），
∴估计在全校学生中任意抽取一个学生，是良好读者的概率=
=；
（2）画树状图得：
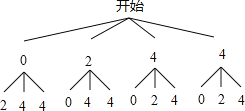
∵共有12种等可能的结果，抽得2人的课外书籍阅读本数都为4的有2种情况，
∴抽得2人的课外书籍阅读本数都为4的概率为：
=．
练习册系列答案
相关题目
