题目内容
【题目】如图，已知抛物线y=ax2+bx+c与x轴的一个交点为A（3，0），与y轴的交点为点B（0，3），其顶点为C，对称轴为x=1，
（1）求抛物线的解析式；
（2）已知点M为y轴上的一个动点，当△ABM为等腰三角形时，求点M的坐标；
（3）将△AOB沿x轴向右平移m个单位长度（0＜m＜3）得到另一个三角形，将所得的三角形与△ABC重叠部分的面积记为S，用m的代数式表示S，并求其最大值．
【答案】（1）y=﹣x2+2x+3（2）（0，0）、（0，﹣3）、（0，3+3
）、（0，3﹣3）（3）当0＜m≤
时，S=﹣m2+3m；当＜m＜3时，S=
m2﹣3m+
【解析】试题分析：（1）根据对称轴可知，抛物线
与x轴的另一个交点为（﹣1，0），根据待定系数法可得抛物线的解析式为
．
（2）分三种情况：①当MA=MB时；②当AB=AM时；③当AB=BM时；三种情况讨论可得点M的坐标．
（3）平移后的三角形记为△PEF．根据待定系数法可得直线AB的解析式为y=﹣x+3．易得AB平移m个单位所得直线EF的解析式为y=﹣x+3+m．根据待定系数法可得直线AC的解析式．连结BE，直线BE交AC于G，则G（，3）．在△AOB沿x轴向右平移的过程中．根据图象，易知重叠部分面积有两种情况：①当
时；②当
时；讨论可得用m的代数式表示S．
试题解析：（1）由题意可知，抛物线与x轴的另一个交点为（﹣1，0），则：
，解得：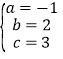
．
故抛物线的解析式为．
（2）依题意：设M点坐标为（0，m），
①当MA=MB时：
，解得m=0，故M（0，0）；
②当AB=AM时：
，解得m=3（舍去）或m=﹣3，故M（0，﹣3）；
③当AB=BM时，
，解得
，故M（0，
）或M（0，
）．
所以点M的坐标为：（0，0）、（0，﹣3）、（0，）、（0，）．
（3）平移后的三角形记为△PEF．设直线AB的解析式为
，则：
，解得：
．
则直线AB的解析式为
．
△AOB沿x轴向右平移m个单位长度（
）得到△PEF，易得直线EF的解析式为
．
设直线AC的解析式为
，则：
，解得：
，
则直线AC的解析式为
．
连结BE，直线BE交AC于G，则G（，3）．
在△AOB沿x轴向右平移的过程中．
①当时，如图1所示．
设PE交AB于K，EF交AC于M．则BE=EK=m，PK=PA=3﹣m，
联立
，解得：
，即点M（3﹣m，2m）．
故S=S△PEF﹣S△PAK﹣S△AFM=
=
．
②当时，如图2所示．
设PE交AB于K，交AC于H．因为BE=m，所以PK=PA=3﹣m，
又因为直线AC的解析式为，所以当
时，得
，所以点H（
，
）．
故S=S△PAH﹣S△PAK=PAPH﹣PA2=
．
综上所述，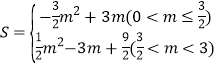
．
