题目内容
【题目】如图1，有若干张边长为
的小正方形①、长为
宽为的长方形②以及边长为的大正方形③的纸片．
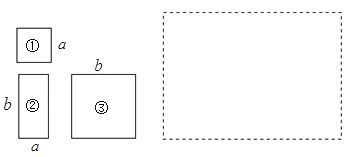
（1）已知小正方形①与大正方形③的面积之和为169，长方形②的周长为34，求长方形②的面积．
（2）如果现有小正方形①1张，大正方形③2张，长方形②3张，请你将它们拼成一个大长方形 （在图2虚线框内画出图形），并运用面积之间的关系，将多项式
分解因式．
【答案】（1）60；（2）
【解析】(1) 由长方形(2)的周长为34,得出,根据题意可以知道:小正方形(1)与大正方形(3)的面积之和为,将两边同时平方,可求得ab的值,从而可求得长方形(2)的面积;
(2). 根据小正方形(1)1张,大正方形(3)2张,长方形(2)3张,直接画出图形,利用图形分解因式即可.
本题解析：
（1）由题意得：
，
，
∴长方形②的面积为60．
（2）如图：
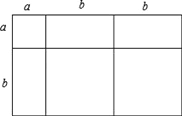
∴a+3ab+2b=(a+2b)(a+b)
练习册系列答案
相关题目
