题目内容
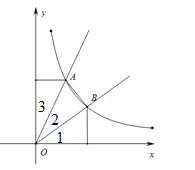
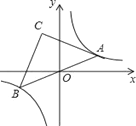
【题目】如图,点A是双曲线![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
A. y=﹣![]() x B. y=﹣
x B. y=﹣![]() x C. y=﹣
x C. y=﹣![]() D. y=﹣
D. y=﹣![]()
【答案】C
【解析】试题解析:连结OC,作CD⊥x轴于D,AE⊥x轴于E,如图,
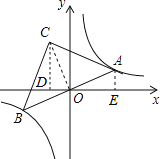
设A点坐标为(a,![]() ),
),
∵A点、B点是正比例函数图象与双曲线y=![]() 的交点,
的交点,
∴点A与点B关于原点对称,
∴OA=OB
∵△ABC为等腰直角三角形,
∴OC=OA,OC⊥OA,
∴∠DOC+∠AOE=90°,
∵∠DOC+∠DCO=90°,
∴∠DCO=∠AOE,
∵在△COD和△OAE中

∴△COD≌△OAE(AAS),
∴OD=AE=![]() ,CD=OE=a,
,CD=OE=a,
∴C点坐标为(-![]() ,a),
,a),
∵-![]() a=-4,
a=-4,
∴点C在反比例函数y=-![]() 图象上.
图象上.
故选C.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
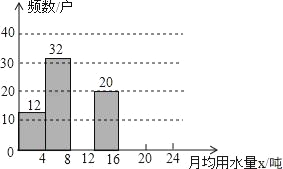
【题目】2014年,河北省委宣传部主办“河北节约之星”活动,表彰节水先进典型,省委宣传部号召全社会以节水先进典型为榜样,牢固树立节约用水理念,争做节俭美德的传承者,节约用水的践行者.小鹏想了解某小区住户月均用水情况,随机调查了该小区部分住户,并将调查数据绘制成如图所示的频数分布直方图(不完整)和如下的频数分布表.
月均用水量x(吨) | 频数(户) | 频率 |
0<x≤4 | 12 | a |
4<x≤8 | 32 | 0.32 |
8<x≤12 | b | c |
12<x≤16 | 20 | 0.2 |
16<x≤20 | 8 | 0.08 |
20<x≤24 | 4 | 0.04 |
(1)求a,b,c的值,并将如图所示的频数分布直方图补充完整;
(2)求月均用水量超过12吨的住户占所调查总住户的百分比;
(3)若该小区有1000住户,根据所调查的数据,该小区月均用水量没有超过8吨的住户有多少?