题目内容
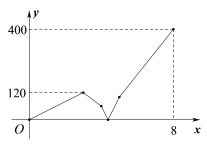
【题目】在一条笔直的公路上顺次有A、B、C三地,甲车从B地出发往A地匀速行驶,到达A地后停止.在甲车出发的同时,乙车也从B地出发往A地匀速行驶,到达A地停留1小时后,调头按原速向C地行驶.若AB两地相距300千米,在两车行驶的过程中,甲、乙两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示,则在两车出发后经过_____小时相遇.
【答案】![]()
【解析】
观察函数图像可知A、C两地的间距,由速度=路程÷时间可求出乙车的速度,结合甲、乙两车速度间的关系可求出甲车的速度,再求出乙车从A地返回时两车的间距,依据相遇时间=4+两车的间距÷两车的速度和,即求出甲、乙两车相遇的时间.
解:最总两车相距400km,
A、C两地相距400km,
乙车的速度为(300+400)÷(8-1)=100km/h,
甲车的速度为100-120÷3=60 km/h,
乙车从A地返回时,两车的间距为300-60×4=60km,
∴两车相遇的时间为4+60÷(100+60)=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目