题目内容
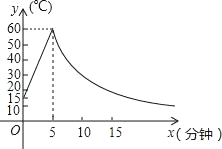
【题目】如图为某种材料温度y（℃）随时间x（min）变化的函数图象．已知该材料初始温度为15℃，温度上升阶段y与时间x成一次函数关系，且在第5分钟温度达到最大值60℃后开始下降；温度下降阶段，温度y与时间x成反比例关系．
（1）分别求该材料温度上升和下降阶段，y与x间的函数关系式；
（2）根据工艺要求，当材料的温度高于30℃时，可以进行产品加工，问可加工多长时间？
【答案】(1) 
,y=
; (2)
min.
【解析】
（1）确定两个函数后，找到函数图象经过的点的坐标，用待定系数法求得函数的解析式即可；
（2）分别令两个函数的函数值为30，解得两个x的值相减即可得到答案．
（1）设温度上升阶段一次函数表达式为y=kx+b（k≠0）．
∵该函数图象经过点（0，15），（5，60），∴
，解得：
，∴一次函数的表达式为y=9x+15（0≤x≤5）．
设温度下降阶段反比例函数表达式为y=
（a≠0）．
∵该函数图象经过点（5，60），∴
=60，解得：a=300，∴反比例函数表达式为y=（x≥5）；
（2）∵y=9x+15，∴当y=30时，9x+15=30，解得：x=
．
∵y=，∴当y=30时，=30，解得：x=10，10﹣=，所以可加工的时间为分钟．
练习册系列答案
相关题目
