��Ŀ����
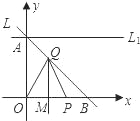
����Ŀ����ͼ��ʾ����ֱ֪��L����A��0��1����B��1��0����P��x���������ϵĶ��㣬OP�Ĵ�ֱƽ���߽�L�ڵ�Q����x���ڵ�M��
��1��ֱ��д��ֱ��L�Ľ���ʽ��
��2����OP��t����OPQ�����ΪS����S����t�ĺ�����ϵʽ���������0��t��2ʱ��S�����ֵ��
��3��ֱ��L1����A����x��ƽ�У�����L1���Ƿ���ڵ�C��ʹ����CPQ����QΪֱ�Ƕ���ĵ���ֱ�������Σ������ڣ������C�����꣬��֤�����������ڣ���˵�����ɣ�
���𰸡���1��y��1��x����2��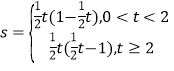 ��S�����ֵ
��S�����ֵ![]() ����3�����ڵ�C��1��1����
����3�����ڵ�C��1��1����
��������
��1����ֱ֪��L��A��B���㣬�ɽ�������������ֱ�ߵĽ���ʽ�У��ô���ϵ�������ֱ��L�Ľ���ʽ��
��2����������OPQ�����������֪���ױ�OP��QM�ij�����֪��OPΪt���ؼ������QM�ij�����֪��QM��ֱƽ��OP����ôOM��![]() t��Ȼ��Ҫ��������ۣ��ٵ�OM��OBʱ����0��t��2ʱ��BM��OB��OM��Ȼ���ڵ���ֱ��������BQM�У����ɵó�QM��BM���ɴ˿ɸ��������ε������ʽ�ó�S��t�ĺ�����ϵʽ���ڵ�OM��OBʱ������t��2ʱ��BM��OM��OB��Ȼ����ݢٵķ������ɵó�S��t�ĺ�����ϵʽ��Ȼ��ɸ���0��t��2ʱ�ĺ������������S�����ֵ��
t��Ȼ��Ҫ��������ۣ��ٵ�OM��OBʱ����0��t��2ʱ��BM��OB��OM��Ȼ���ڵ���ֱ��������BQM�У����ɵó�QM��BM���ɴ˿ɸ��������ε������ʽ�ó�S��t�ĺ�����ϵʽ���ڵ�OM��OBʱ������t��2ʱ��BM��OM��OB��Ȼ����ݢٵķ������ɵó�S��t�ĺ�����ϵʽ��Ȼ��ɸ���0��t��2ʱ�ĺ������������S�����ֵ��
��3��������������ĵ�C����ôCQ��QP��OQ�����C��O����ֱ��BL�Գƣ����C������Ӧ���ǣ�1��1������ôֻ��֤��CQ��PQ���ɣ�����������������ۣ��ٵ�Q���߶�AB�ϣ�Q��B���غϣ�����P���߶�OB��ʱ��Ҫ֤��CQP��90������ô���ı���CQPB�У�������֤����QCB���QPB���������ڡ�QPB���QPO����������QPO����QOP�����ֻ��֤��QCB����QOB���ɣ������۵������ʣ�����������ȣ��ɴ˿ɵ�֤���ڵ�Q���߶�AB�ϣ�P��OB���ӳ�����ʱ�����ݢ��ѵó���QPB����QCB����ô�������Ƕ�����һ����ȵĶԶ��Ǻɵó���CQP����CBP��90�ȣ��۵�Q��B�غ�ʱ������Ȼ��������CQPӦ���Ǹ�����ֱ�������Σ������������ɵó���������C������꣮
��1��y��1��x��
��2����OP��t��
��Q��ĺ�����Ϊ![]() t��
t��
�ٵ�![]() ����0��t��2ʱ��QM=1-
����0��t��2ʱ��QM=1-![]() t��
t��
��S��OPQ��![]() t��1��
t��1��![]() t����
t����
�ڵ�t��2ʱ��QM��|1��![]() t|��
t|��![]() t��1��
t��1��
��S��OPQ��![]() t��
t��![]() t��1����
t��1����
��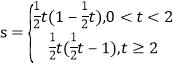
��0��![]() t��1����0��t��2ʱ��S��
t��1����0��t��2ʱ��S��![]() t��1��
t��1��![]() t������
t������![]() ��t��1��2+
��t��1��2+![]() ��
��
�൱t��1ʱ��S�����ֵ![]() ��
��
��3����OA��OB��1������OAB�ǵ���ֱ�������Σ�
����L1�ϴ��ڵ�C��ʹ����CPQ����QΪֱ�Ƕ���ĵ���ֱ�������Σ�
��PQ��QC��
����OQ��QC����L1��x�ᣬ��C��O�������ֱ��L�Գƣ�
����AC��OA��1����C��1��1��������֤��PQC��90�ȣ���CB�����ı���OACB�������Σ�
�ٵ���P���߶�OB�ϣ�Q���߶�AB�ϣ�Q��B��C���غϣ�ʱ����ͼ��1��
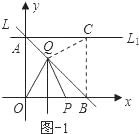
�ɶԳ��ԣ��á�BCQ����QOP����QPO����QOP��
���QPB+��QCB����QPB+��QPO��180����
���PQC��360��������QPB+��QCB+��PBC����90�ȣ�
�ڵ���P���߶�OB���ӳ����ϣ�Q���߶�AB��ʱ����ͼ��2����ͼ��3
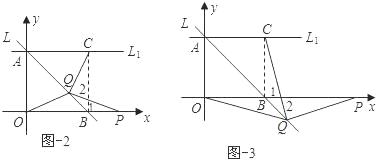
�ߡ�QPB����QCB����1����2��
���PQC����PBC��90�ȣ�
�۵���Q���B�غ�ʱ����Ȼ��PQC��90�ȣ�
�ۺϢ٢ڢۣ���PQC��90�ȣ�
����L1�ϴ��ڵ�C��1��1����ʹ�á�CPQ����QΪֱ�Ƕ���ĵ���ֱ�������Σ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�