Question

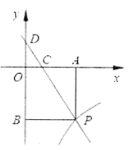
【题目】如图，直线y=6与双曲线y=（k≠0，且>0）交点A，点A的横坐标为2．

（1）求点A的坐标及双曲线的解析式；

（2）点B是双曲线上的点，且点B的纵坐标是6，连接OB，AB．求三角形△AOB的面积．

Answer 1

【答案】（1）A(2,12),；（2）18.

【解析】分析：

（1）把x=2代入y=6x可得y=12，由此可得点A的坐标为（2，12），将点A的坐标代入中可解得k=24，由此即可得到反比例函数的解析式；

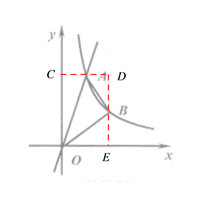
（2）如图，由（1）中所得反比例函数的解析式易得点B的坐标为（4，6），过A作y轴的垂线AC，过点B作x轴的垂线BE，两条垂线相交于点D，由S△AOB=S矩形OEDC-S△OEB-S△ABD-S△AOC结合已知条件即可求得△AOB的面积.

详解：

（1）∵在y=6x中，当x=2时，y=12,

∴点A的坐标为(2,12),

将点A的坐标代入 得：则k=24，

∴反比例函数的解析式为： ；

（2）∵点B在反比例函数的图象上，且点B的纵坐标为6，

∴，解得：，

∴点B的坐标为：（4，6），

如下图，过A作y轴的垂线AC，过点B作x轴的垂线BE，两条垂线相交于点D，

∴C（0，12），D（4，12），E（4，0），

==18.