��Ŀ����
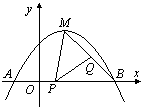
��ͼ��������y1=ax2-2ax+b����A(-1��0)���� C(2��![]() )���㣬��x�ύ����һ��B��
)���㣬��x�ύ����һ��B��
�� (1) ��˒����ߵĽ���ʽ��
�� (2) �������ߵĶ���ΪM����PΪ�߶�OB��һ����(�����B�غ�)����Q���߶�MB���ƶ�������MPQ=45�㣬���߶�OP=x��MQ=![]() y2����y2��x�ĺ�����ϵʽ����ֱ��д���Ա���x��ȡֵ��Χ��
y2����y2��x�ĺ�����ϵʽ����ֱ��д���Ա���x��ȡֵ��Χ��
�� (3) ��ͬһƽ��ֱ������ϵ�У�����ֱ��x=m��x=n�ֱ��뒁���߽��ڵ�E��G����(2)�е�
���� ����ͼ���ڵ�F��H�����ı���EFHG�ܷ�Ϊƽ���ı��Σ����ܣ���m��n֮���������ϵ�������ܣ���˵�����ɡ�
 |
�⣺(1) �ߒ�����y1=ax2-2ax+b����A(-1��0)��C(0��![]() )���㣬��
)���㣬��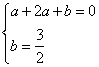 ����a= -
����a= -![]() ��
��
�� ������b=![]() ���������ߵĽ���ʽΪy1= -
���������ߵĽ���ʽΪy1= -![]() x2+x+
x2+x+![]() ��
��
�� (2) ��MN��AB������ΪN����y1= -![]() x2+x+
x2+x+![]() ��M(1��2)�� N(1��0)��A(-1��0)��B(3��0)����AB=4��MN=BN=2��MB=2
��M(1��2)�� N(1��0)��A(-1��0)��B(3��0)����AB=4��MN=BN=2��MB=2![]() ����MBN=45�㡣���ݹ��ɶ�����BM 2-BN 2=PM 2-PN 2��
����MBN=45�㡣���ݹ��ɶ�����BM 2-BN 2=PM 2-PN 2��
���� ��(2![]() )2-22=PM2= -(1-x)2��j������MPQ=45��=��MBP��
)2-22=PM2= -(1-x)2��j������MPQ=45��=��MBP��
���� ���MPQ~��MBP����PM2=MQ?MB=![]() y2?2
y2?2![]() ��k��
��k��
���� ��j��k��y2=![]() x2-x+
x2-x+![]() ����0��x<3����y2��x�ĺ�����ϵʽΪy2=
����0��x<3����y2��x�ĺ�����ϵʽΪy2=![]() x2-x+
x2-x+![]() (0��x<3)��
(0��x<3)��
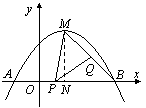
(3) �ı���EFHG����Ϊƽ���ı��Σ�m��n֮���������ϵ��
���� m+n=2(0��m��2����m¹1)���ߵ�E��G��������y1= -![]() x2+x+
x2+x+![]()
���� �ֱ���ֱ��x=m��x=n�Ľ��㣬���E��G����Ϊ
���� E(m��-![]() m2+m+
m2+m+![]() )��G(n��-
)��G(n��-![]() n2+n+
n2+n+![]() )��ͬ������F��H����
)��ͬ������F��H����
���� ΪF(m��![]() m2-m+
m2-m+![]() )��H(n��
)��H(n��![]() n2-n+
n2-n+![]() )��
)��
���� ��EF=![]() m2-m+
m2-m+![]() -(-
-(-![]() m2+m+
m2+m+![]() )=m2-2m+1��GH=
)=m2-2m+1��GH=![]() n2-n+
n2-n+![]() -(-
-(-![]() n2+n+
n2+n+![]() )=n2-2n+1��
)=n2-2n+1��
���� ���ı���EFHG��ƽ���ı��Σ�EF=GH����m2-2m+1=n2-2n+1����(m+n-2)(m-n)=0��
���� ������֪m��n����m+n=2 (0��m��2����m��1)��
���� ��ˣ��ı���EFHG����Ϊƽ���ı��Σ�m��n֮���������ϵ��m+n=2 (0��m��2����m��1)��
 |

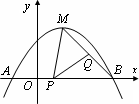
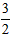 �����㣬��x�ύ����һ��B��
�����㣬��x�ύ����һ��B��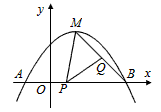
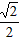 y2����y2��x�ĺ�����ϵʽ����ֱ��д���Ա���x��ȡֵ��Χ��
y2����y2��x�ĺ�����ϵʽ����ֱ��д���Ա���x��ȡֵ��Χ��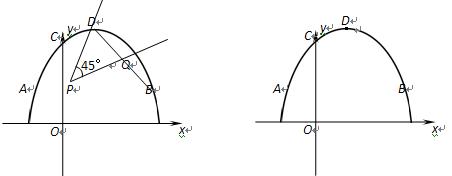
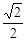 y2´2
y2´2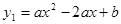 �Ķ���ΪD����x�ύ�ڵ�A��B����y�ύ�ڵ�C����OB = 2OC= 3��
�Ķ���ΪD����x�ύ�ڵ�A��B����y�ύ�ڵ�C����OB = 2OC= 3��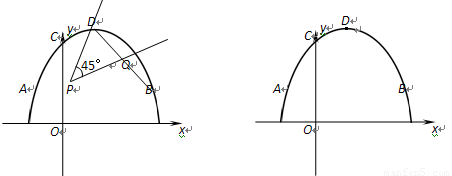
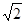 DQ�������y2����x�ĺ�����ϵʽ��
DQ�������y2����x�ĺ�����ϵʽ��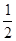 �ֱ���������y1���ڵ�E��G����y2�ĺ���ͼ���ڵ�F��H���ʵ�E��F��H��GΧ���ı��ε�����ܷ�Ϊ
�ֱ���������y1���ڵ�E��G����y2�ĺ���ͼ���ڵ�F��H���ʵ�E��F��H��GΧ���ı��ε�����ܷ�Ϊ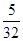 �����ܣ����m��ֵ�������ܣ���˵�����ɣ�
�����ܣ����m��ֵ�������ܣ���˵�����ɣ� )���㣬��������ߵĽ���ʽ��
)���㣬��������ߵĽ���ʽ��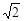 ���ɸ��ݹ��ɶ�����jPD2-(1-x)2=4������Ϊ��MPQ
�� ��MBP������kPD2=DQ´DB=
���ɸ��ݹ��ɶ�����jPD2-(1-x)2=4������Ϊ��MPQ
�� ��MBP������kPD2=DQ´DB=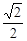 y2´2
y2´2