题目内容
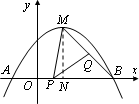
如图,拋物线y1=ax2-2ax+b经过A(-1,0),C(2,![]() )两点,与x轴交于另一点B;
)两点,与x轴交于另一点B;
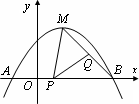
(1)求此拋物线的解析式;
(2)若拋物线的顶点为M,点P为线段OB上一动点(不与点B重合),点Q在线段MB上移动,且∠MPQ=45°,设线段OP=x,MQ=![]() y2,求y2与x的函数关系式,并直接写出自变量x的取值范围;
y2,求y2与x的函数关系式,并直接写出自变量x的取值范围;
(3)在同一平面直角坐标系中,两条直线x=m,x=n分别与拋物线交于点E,G,与(2)中的函数图像交于点F,H.问四边形EFHG能否为平行四边形?若能,求m,n之间的数量关系;若不能,请说明理由.
解析:
|
解∶(1)∵拋物线y1=ax2-2ax+b经过A(-1,0),C(0, (2)作MN⊥AB,垂足为N.由y1=- N(1,0),A(-1,0),B(3,0),∴AB=4,MN=BN=2,MB=2 ∠MBN=45°.根据勾股定理有BM2-BN2=PM2-PN2. ∴(2 ∴△MPQ∽△MBP,∴PM2=MQ×MB= 由①、②得y2=
(3)四边形EFHG可以为平行四边形,m、n之间的数量关系是m+n=2(0≤m≤2,且m≠1).∵点E、G是抛物线y1=- 分别与直线x=m,x=n的交点,∴点E、G坐标为 E(m,- 为F(m, ∴EF= ∵四边形EFHG是平行四边形,EF=GH.∴m2-2m+1=n2-2n+1,∴(m+n-2)(m-n)=0. 由题意知m≠n,∴m+n=2(0≤m≤2,且m≠1). 因此,四边形EFHG可以为平行四边形,m、n之间的数量关系是m+n=2(0≤m≤2,且m≠1).
|

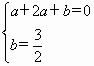 ,∴a=-
,∴a=-