题目内容
【题目】已知AB=AC,BD=DC,AE平分∠FAB,问:AE与AD是否垂直?为什么? 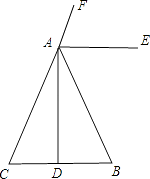
【答案】证明:∵AB=AC,CD=BD,
∴∠1=∠2,∠B=∠C,AD⊥BC,
又∵AE是△ABC的外角平分线,
∴∠3=∠4= ![]() (∠B+∠C)=∠C,
(∠B+∠C)=∠C,
∴AE∥BC,∠DAE+∠ADB=180°,
又∵AD⊥BC,
∴∠DAE=∠ADC=90°.
∴AE⊥AD.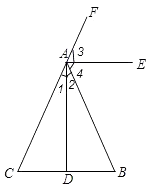
【解析】根据等腰三角形的性质可知,∠1=∠2,∠B=∠C,由三角形外角平分线的性质可知∠3=∠C,AE∥BC,由平行线的性质可知AE⊥AD.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,以及对等腰三角形的性质的理解,了解等腰三角形的两个底角相等(简称:等边对等角).

练习册系列答案
相关题目