题目内容
一个三角形的三边长分别为
,
,2
,(
>0),则这个三角形的面积是______.
| 16m2+n2 |
| 4m2+9n2 |
| m2+n2 |
| n |
| m |
设三角形中,a=2
,b=
,c=
.
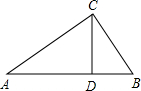
作AD⊥BC于D,设CD=x.
根据勾股定理,得
(
)2-x2=(
)2-(2
-x)2,
解得
x=
.
则这个三角形的面积是
×2
×
=
=5mn.

| m2+n2 |
| 16m2+n2 |
| 4m2+9n2 |
作AD⊥BC于D,设CD=x.
根据勾股定理,得
(
| 16m2+n2 |
| 4m2+9n2 |
| m2+n2 |
解得
x=
| 4m2-n2 | ||
|
则这个三角形的面积是
| 1 |
| 2 |
| m2+n2 |
16m2+n2-
|
| 25m2n2 |


练习册系列答案
相关题目