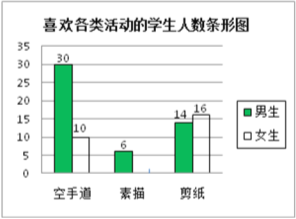
题目内容
【题目】如图1,四边形ABCD中,AD∥BC,AB⊥BC,点E在边AB上,∠DEC=900,且DE=EC.
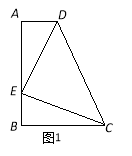
(1)求证:△ADE≌△BEC;
(2)若AD=a,AE=b,DE=c,请用图1证明勾股定理:a2+b2=c2;
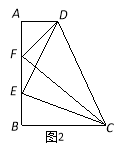
(3)线段AB上另有一点F(不与点E重合),且DF⊥CF(如图2),若AD=2,BC=4,求EF的长.
【答案】(1)、证明过程见解析;(2)、证明过程见解析;(3)、2.
【解析】
试题分析:(1)、根据∠DEC=90°得出∠AED+∠CEB=90°,结合∠ADE+∠AED=90°得出∠ADE=∠CEB,从而说明三角形全等;(2)、根据图形得出△ADE,△DEC,△BEC都是直角三角形,然后根据全等得出BE=a,BC=b,然后根据面积相等的法则得出答案;(3)、根据题意得出△AFD和△BCF相似,设AF=x,则BF=6-x,从而求出x的值,然后得出EF的长度.
试题解析:(1)如图1,∵∠DEC=90°,∴∠AED+∠CEB=90°,∵∠ADE+∠AED=90°,
∴∠ADE=∠CEB,
在△ADE和△BEC中, ,∴△ADE≌△BEC(AAS);
,∴△ADE≌△BEC(AAS);
(2)、如图1,∵AB⊥BC,∠DEC=90°,∴△ADE,△DEC,△BEC都是直角三角形,
∵AD=a,AE=b,DE=c,且DE=EC,△ADE≌△BEC,∴BE=a,BC=b,
∴![]() (a+b)(a+b)=
(a+b)(a+b)=![]() ab+
ab+![]() c2+
c2+![]() ab,
ab,
整理得:a2+b2=c2;
(3)、如图2,由(1)得:△ADE≌△BEC(AAS),则AD=BE=2,BC=AE=4,
∵DF⊥CF, ∴∠AFD+∠BFC=90°,∵∠BFC+∠BCF=90°,∴∠AFD=∠BCF,又∵∠A=∠B,
∴△AFD∽△BCF,∴![]() ,设AF=x,则BF=6﹣x,故
,设AF=x,则BF=6﹣x,故![]() ,
,
解得:x1=2,x2=4, ∵点F不与点E重合, ∴x=2,∴EF=6﹣2﹣2=2.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案【题目】观察下列算式:
21=2,22=4,23=8,24=16,25=32,26=64, 27=128,28=256,…根据上述算式中的规律,你认为220的末位数字是 .
A | 2 | -4 | 9 | -10 |
B | 3 | 3 | -7 | 9 |
C | 6 | 12 | 63 | 90 |