题目内容
(2012•绍兴三模)在直角梯形OABC中,OA∥BC,A、B两点的坐标分别为A(13,0),B(11,12),动点P、Q同时从O、B两点出发,点P以每秒2个单位的速度沿OA向终点A运动,点Q以每秒1个单位的速度沿BC向C运动,当点P停止运动时,点Q同时停止运动.线段OB、PQ相交于点D,过点D作DE∥OA,交AB于点E,射线QE交x轴于点F(如图).设动点P、Q运动时间为t(单位:秒),则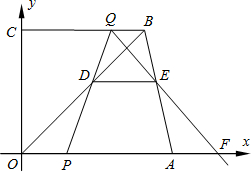 :
:
(1)当t=
时,四边形PABQ是平行四边形;
(2)当t=
 :
:(1)当t=
| 13 |
| 3 |
| 13 |
| 3 |
(2)当t=
2或1或
或
| 16 |
| 3 |
| 3 |
| 2 |
2或1或
或
时,△PQF是等腰三角形.| 16 |
| 3 |
| 3 |
| 2 |
分析:(1)设OP=2t,QB=t,PA=13-2t,根据平行四边形的性质(对边平行且相等)知,只需QB=PA,从而求得t;
(2)根据平行线分线段成比例求得
=
=
;然后由平行线OB∥DE∥PA分线段成比例求得
=
;利用等量代换求得AF=2QB=2t,PF=OA=13;分三种情况解答:①QP=FQ,作QG⊥x轴于G,则11-t-2t=2t+13-(11-t);②PQ=FP;③FQ=FP.
(2)根据平行线分线段成比例求得
| QB |
| OP |
| QD |
| DP |
| 1 |
| 2 |
| QB |
| AF |
| 1 |
| 2 |
解答:解:(1)设OP=2t,QB=t,PA=13-2t,
要使四边形PABQ为平行四边形,则13-2t=t
解得t=
.
(2)∵
=
=
,
∵QB∥DE∥PA,
∴
=
;,
∴AF=2QB=2t,
∴PF=OA=13,
①QP=FQ,作QG⊥x轴于G,则11-t-2t=2t+13-(11-t),
∴t=
;
②PQ=FP,
∴
=13,
∴t=2或
;
③FQ=FP,
=13,
∴t=1.
综上,当t=
或2或1或
时,△PQF是等腰三角形.
故答案为:
;2或1或
或
.
要使四边形PABQ为平行四边形,则13-2t=t
解得t=
| 13 |
| 3 |
(2)∵
| QB |
| OP |
| QD |
| DP |
| 1 |
| 2 |
∵QB∥DE∥PA,
∴
| QB |
| AF |
| 1 |
| 2 |
∴AF=2QB=2t,
∴PF=OA=13,
①QP=FQ,作QG⊥x轴于G,则11-t-2t=2t+13-(11-t),
∴t=
| 3 |
| 2 |
②PQ=FP,
∴
| (11-3t)2+122 |
∴t=2或
| 16 |
| 3 |
③FQ=FP,
| [13+2t-(11-t)]2+122 |
∴t=1.
综上,当t=
| 3 |
| 2 |
| 16 |
| 3 |
故答案为:
| 13 |
| 3 |
| 16 |
| 3 |
| 3 |
| 2 |
点评:本题综合考查了平行线分线段成比例、平行四边形的判定、等腰三角形的判定及勾股定理与直角梯形性质的应用.解答此题时,多处用到了分类讨论的数学思想,防止漏解.

练习册系列答案
相关题目
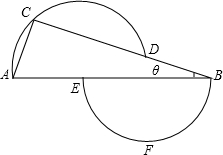 (2012•绍兴三模)如图,点D、E分别在∠ABC的边BC、AB上,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=63°,设∠ABC=θ,那么θ=
(2012•绍兴三模)如图,点D、E分别在∠ABC的边BC、AB上,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=63°,设∠ABC=θ,那么θ=