题目内容
(2012•绍兴三模)已知抛物线y1=a1x2+b1x+c1,y2=a2x2+b2x+c2,且满足
=
=
=k(k≠0,1).则称抛物线y1,y2互为“友好抛物线”,则下列关于“友好抛物线”的说法不正确的是( )
| a1 |
| a2 |
| b1 |
| b2 |
| c1 |
| c2 |
分析:根据题中给出的“友好抛物线”的定义结合二次函数的性质对各选项进行逐一判断即可.
解答:解:A、当a1与a2符号相反时其开口方向相反,当|a1|≠|a2|时,两抛物线开口大小不同,故本选项正确;
B、∵
=
=
=k(k≠0,1),∴-
=-
,∴y1与y2的对称轴相同,故本选项正确;
C、∵y1与x轴有两个不同的交点,∴△=b12-4a1c1>0,∵抛物线y2中,△=b22-4a2c2=(b12-4a1c1)/k2>0,故选项正确;
D、∵如果y2的最值是m,∴y1的最值是
=k•
=km,当k<0时,y1的最小值为km.故选项错误.
故选D.
B、∵
| a1 |
| a2 |
| b1 |
| b2 |
| c1 |
| c2 |
| b1 |
| 2a1 |
| b2 |
| 2a2 |
C、∵y1与x轴有两个不同的交点,∴△=b12-4a1c1>0,∵抛物线y2中,△=b22-4a2c2=(b12-4a1c1)/k2>0,故选项正确;
D、∵如果y2的最值是m,∴y1的最值是
4a1c1-
| ||
| 4a1 |
4a2c2-
| ||
| 4a2 |
故选D.
点评:本题考查的是二次函数的性质,先根据题意理解“友好抛物线”的定义是解答此题的关键.

练习册系列答案
相关题目
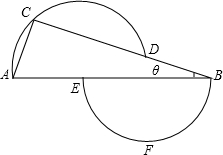 (2012•绍兴三模)如图,点D、E分别在∠ABC的边BC、AB上,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=63°,设∠ABC=θ,那么θ=
(2012•绍兴三模)如图,点D、E分别在∠ABC的边BC、AB上,过D、A、C三点的圆的圆心为E,过B、E、F三点的圆的圆心为D,如果∠A=63°,设∠ABC=θ,那么θ=