题目内容
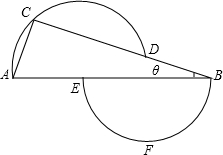（2012•绍兴三模）如图，点D、E分别在∠ABC的边BC、AB上，过D、A、C三点的圆的圆心为E，过B、E、F三点的圆的圆心为D，如果∠A=63°，设∠ABC=θ，那么θ=18
18
°．分析：首先连接DE，CE，由AE=CE=DE，DE=DB，根据等边对等角与三角形外角的性质，可求得∠ECA=∠A=63°，∠ECD=2θ，又由三角形内角和定理，可得方程63+63+2θ+θ=180，继而求得答案．
解答：
解：连接DE，CE，
∵AE=CE=DE，
∴∠ECA=∠A=63°，∠ECD=∠EDC，
∵DE=DB，
∴∠DEB=∠DBE=θ，
∴∠EDC=∠DEB+∠DBE=2θ，
∴∠ECD=2θ，
∵∠A+∠ACD+∠ABC=180°，
∴63+63+2θ+θ=180，
解得：θ=18°．
故答案为：18°．
解：连接DE，CE，∵AE=CE=DE，
∴∠ECA=∠A=63°，∠ECD=∠EDC，
∵DE=DB，
∴∠DEB=∠DBE=θ，
∴∠EDC=∠DEB+∠DBE=2θ，
∴∠ECD=2θ，
∵∠A+∠ACD+∠ABC=180°，
∴63+63+2θ+θ=180，
解得：θ=18°．
故答案为：18°．
点评：此题考查了等腰三角形、三角形外角的性质以及三角形内角和定理．注意掌握辅助线的作法，注意数形结合思想与方程思想的应用．
练习册系列答案
相关题目
