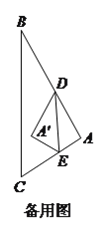题目内容
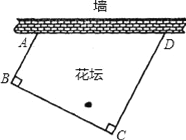
【题目】如图1,已知菱形![]() 的边长为12,
的边长为12,![]() , 点
, 点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的动点(不与端点重合),且
上的动点(不与端点重合),且![]() .
.
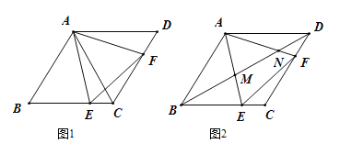
(1)求证: ![]() 是等边三角形;
是等边三角形;
(2)点![]() 、
、![]() 在运动过程中,四边形
在运动过程中,四边形![]() 的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
的面积是否变化,如果变化,请说明理由;如果不变,请求出面积;
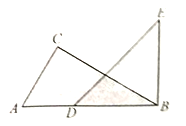
(3)如图2,连接![]() 分别与边
分别与边![]() 、
、![]() 交于
交于![]() 、
、![]() ,当
,当![]() 时,求证:
时,求证:![]()
![]() .
.
【答案】(1)见解析;(2)不变,![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)证明△ACE≌△ADF,证出AE=AF,结合![]() ,便证出△AEF是等边三角形;
,便证出△AEF是等边三角形;
(2)根据△ACE≌△ADF,则四边形![]() 的面积等于△ABC或者△ACD的面积.
的面积等于△ABC或者△ACD的面积.
(3)将△ADN绕点A顺时针旋转120°得到△ABP,连接PM.结合旋转的性质证明△MAN≌△MAP,根据四边形ABCD是菱形,∠ABC=60°,推出∠BPM=90°,即可证明结论.
(1)在菱形ABCD中,∵∠B=60°,
∴△ABC是等边三角形,∠D=∠B=60°,
∴AB=BC=AC,∠ACB=60°,
∴AC=AD,
∵![]() ,
,
∴∠CAE=∠DAF,
又∵∠D=∠ACE=60°,
∴△ACE≌△ADF,
∴AE=AF,
∴△AEF是等边三角形;
(2)点![]() 、
、![]() 在运动过程中,四边形
在运动过程中,四边形![]() 的面积不变.
的面积不变.
理由:
∵△ACE≌△ADF,
∴![]() ,即
,即![]()
![]() ;
;
(3)将△ADN绕点A顺时针旋转120°得到△ABP,连接PM.
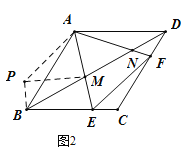
∵∠DAF=15°,∠EAF=60°,∠BAD=120°,
∴∠BAE=45°,∠BAP=∠DAF=15°,
∴∠MAN=∠MAP=60°,
∵AM=AM,AN=AP,
∴△MAN≌△MAP(SAS),
∴MN=PM,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠ADN=![]() ∠ADC=30°,
∠ADC=30°,
∴∠AND=180°-15°-30°=135°,∠ANM=45°,
∴∠APB=∠AND=135°,∠APM=∠ANM=45°,
∴∠BPM=90°,
∴BP2+PM2=BM2,
∵BP=DN,PM=MN,
∴DN2+MN2=BM2.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案【题目】某地农民一直保持着冬种油菜的习惯,利用农闲冬种一季油菜.该地农业部门对2017年的油菜籽生产成本、市场价格、种植面积和产量等进行了调查统计,并绘制了如下的统计表与统计图(如图):
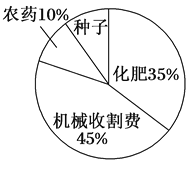
每亩生产成本 | 每亩产量 | 油菜籽市场价格 | 种植面积 |
110元 | 130千克 | 3元/千克 | 500 000亩 |
请根据以上信息解答下列问题:
(1)种植油菜每亩的种子成本是多少元?
(2)农民冬种油菜每亩获利多少元?
(3)2017年该地全县农民冬种油菜的总获利是多少元?(结果用科学记数法表示)