题目内容
如图,A( ,1),B(1,
,1),B(1, ),将∆AOB绕点O旋转1500后,得到∆A’OB’,则此时点A的对应点A’的坐标为()
),将∆AOB绕点O旋转1500后,得到∆A’OB’,则此时点A的对应点A’的坐标为()

 ,1),B(1,
,1),B(1, ),将∆AOB绕点O旋转1500后,得到∆A’OB’,则此时点A的对应点A’的坐标为()
),将∆AOB绕点O旋转1500后,得到∆A’OB’,则此时点A的对应点A’的坐标为()
A.(- ,1) ,1) | B.(-2,0) |
C.(-1,- )或(-2,0) )或(-2,0) | D.(- ,-1)或(-2,0) ,-1)或(-2,0) |
C.
试题分析:∵A(
 ,1),B(1,
,1),B(1, ),
),∴tanα=
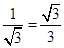 ,
,∴OA与x轴正半轴夹角为30°,OB与y轴正半轴夹角为30°,
∴∠AOB=90°-30°-30°=30°,
根据勾股定理,
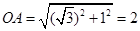 ,
,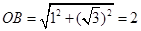 ,
,①如图1,顺时针旋转时,
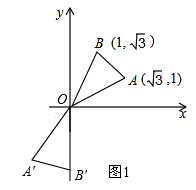
∵150°+30°=180°,
∴点A′、B关于原点O成中心对称,
∴点A′(-1,-
 );
);②如图2,逆时针旋转时,
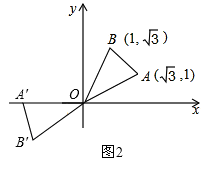
∵150°+30°=180°,
∴点A′在x轴负半轴上,
∴点A′的坐标是(-2,0).
综上所述,点A′的坐标为(-1,-
 )或(-2,0).
)或(-2,0).故选C.
考点: 坐标与图形变化-旋转.

练习册系列答案
相关题目

 ∠ABC(0°<∠CBE<
∠ABC(0°<∠CBE<

 的三个顶点都在格点上(每个小方格的顶点叫格点).
的三个顶点都在格点上(每个小方格的顶点叫格点).
 的值为( )
的值为( )







 和△
和△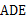 都是等腰直角三角形,∠
都是等腰直角三角形,∠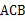 和∠
和∠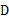 都是直角,点
都是直角,点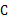 在
在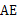 上,△
上,△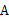 点经过逆时针旋转后能够与△
点经过逆时针旋转后能够与△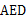 重合,再将图(1)作为“基本图形”绕着
重合,再将图(1)作为“基本图形”绕着