题目内容
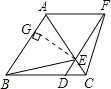
【题目】如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、BE和CF.
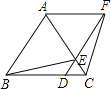
(1)请在图中找出一对全等三角形,用符号“≌”表示,并加以证明;
(2)判断四边形ABDF是怎样的四边形,并说明理由;
(3)若AB=6,BD=2DC,求四边形ABEF的面积..
【答案】(1)见解析;(2)平行四边形;(3)![]()
【解析】试题分析:(1)从图上及已知条件容易看出△BDE≌△FEC,△BCE≌△FDC,△ABE≌△ACF.判定两个三角形全等时,必须有边的参与,所以此题的关键是找出相等的边.
(2)由(1)的结论容易证明AB∥DF,BD∥AF,两组对边分别平行的四边形是平行四边形.
(3)EF∥AB,EF≠AB,四边形ABEF是梯形,只要求出此梯形的面积即可.
试题解析:解:(1)△BDE≌△FEC或△BCE≌△FDC或△ABE≌△ACF.
(选证一)△BDE≌△FEC.
证明:∵△ABC是等边三角形,∴BC=AC,∠ACB=60°.
∵CD=CE,∴△EDC是等边三角形,∴DE=EC,∠CDE=∠DEC=60°,∴∠BDE=∠FEC=120°.
又∵EF=AE,∴BD=FE,∴△BDE≌△FEC.
(选证二)△BCE≌△FDC.
证明:∵△ABC是等边三角形,∴BC=AC,∠ACB=60°.
又∵CD=CE,∴△EDC是等边三角形,∴∠BCE=∠FDC=60°,DE=CE.
∵EF=AE,∴EF+DE=AE+CE,∴FD=AC=BC,∴△BCE≌△FDC.
(选证三)△ABE≌△ACF.
证明:∵△ABC是等边三角形,∴AB=AC,∠ACB=∠BAC=60°.
∵CD=CE,∴△EDC是等边三角形,∴∠AEF=∠CED=60°.
∵EF=AE,△AEF是等边三角形,∴AE=AF,∠EAF=60°,∴△ABE≌△ACF.
(2)由(1)知,△ABC、△EDC、△AEF都是等边三角形,∴∠CDE=∠ABC=∠EFA=60°,∴AB∥DF,BD∥AF,∴四边形ABDF是平行四边形.
(3)由(2)知,四边形ABDF是平行四边形,∴EF∥AB,EF≠AB,∴四边形ABEF是梯形.
过E作EG⊥AB于G,则EG=![]() ,∴
,∴![]()
![]() .
.